题目内容
3.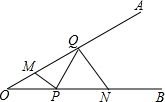 如图,∠AOB=30°,M,N分别是边OA,OB上的定点,P、Q分别是边OB,OA上的动点,记∠AMP=∠1,∠ONQ=∠2,当MP+PQ+QN最小时,则关于∠1,∠2的数量关系正确的是( )
如图,∠AOB=30°,M,N分别是边OA,OB上的定点,P、Q分别是边OB,OA上的动点,记∠AMP=∠1,∠ONQ=∠2,当MP+PQ+QN最小时,则关于∠1,∠2的数量关系正确的是( )| A. | ∠1+∠2=90° | B. | 2∠2-∠1=30° | C. | 2∠1+∠2=180° | D. | ∠1-∠2=90° |
分析 如图,作M关于OB的对称点M′,N关于OA的对称点N′,连接M′N′交OA于Q,交OB于P,则MP+PQ+QN最小,根据外角的性质得到∠1=∠O+∠OPM,∠OPM=∠1-∠O=∠1-30°,由轴对称的性质得到∠OPM=∠OPM′,∠OPM′=∠QPN,于是得到∠QPN=∠1+30°,由于∠3=∠O+∠2=30°+∠2,∠NQN′=∠QPN+∠2=∠1-30°+∠2,∠NQN′=2∠3,即可得到结论.
解答  解:如图,作M关于OB的对称点M′,N关于OA的对称点N′,连接M′N′交OA于Q,交OB于P,则MP+PQ+QN最小,
解:如图,作M关于OB的对称点M′,N关于OA的对称点N′,连接M′N′交OA于Q,交OB于P,则MP+PQ+QN最小,
∵∠1=∠O+∠OPM,
∴∠OPM=∠1-∠O=∠1-30°,
∵∠OPM=∠OPM′,∠OPM′=∠QPN,
∴∠QPN=∠PQO+30°
∵∠3=∠O+∠2=30°+∠2,∠NQN′=∠QPN+∠2=∠1-30°+∠2,∠NQN′=2∠3,
∴∠1-30°+∠2=2(30°+∠2),
∴∠1-∠2=90°.
故选D.
点评 本题考查了轴对称-最短路线问题,三角形的外角的性质,正确的作出图形是解题的关键.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
13.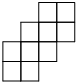 将数字2放入图中的10个小方格中,则数字2放在两个“田”字形重叠方格的概率是( )
将数字2放入图中的10个小方格中,则数字2放在两个“田”字形重叠方格的概率是( )
 将数字2放入图中的10个小方格中,则数字2放在两个“田”字形重叠方格的概率是( )
将数字2放入图中的10个小方格中,则数字2放在两个“田”字形重叠方格的概率是( )| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{2}{5}$ |
18.在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一直线上,当△ABC的周长最小时,点C的坐标可能是( )
| A. | (0,0) | B. | (0,-1) | C. | (0,5) | D. | (0,3) |
15.下列汉字是轴对称图形的是( )
| A. | 王 | B. | 国 | C. | 洋 | D. | 告 |
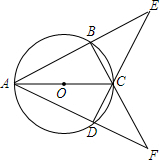 如图,四边形ABCD内接于⊙O,AB与DC的延长线交于点E,AD与BC的延长线交于点F.若∠E=∠F=44°.
如图,四边形ABCD内接于⊙O,AB与DC的延长线交于点E,AD与BC的延长线交于点F.若∠E=∠F=44°. 如图,在四边形ABCD,AB⊥BC,AC⊥CD,AB=2,CD=8,tan∠BAC=2,求tanD的值.
如图,在四边形ABCD,AB⊥BC,AC⊥CD,AB=2,CD=8,tan∠BAC=2,求tanD的值.