题目内容
6.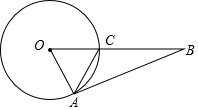 如图,OA,OC都是⊙O的半径,点B在OC的延长线上,BA与⊙O相切于点A,连接AC,若AC=2,tan∠BAC=$\frac{1}{2}$,则⊙O的半径长为$\sqrt{5}$.
如图,OA,OC都是⊙O的半径,点B在OC的延长线上,BA与⊙O相切于点A,连接AC,若AC=2,tan∠BAC=$\frac{1}{2}$,则⊙O的半径长为$\sqrt{5}$.
分析 作直径AD,连接CD,如图,利用圆周角定理得到∠ACD=90°,再根据切线的性质得∠DAB=90°,则利用等角的余角相等得到∠D=∠BAC,所以tanD=tan∠BAC=$\frac{1}{2}$,然后在Rt△ACD中利用正切定义可计算出CD=4,利用勾股定理可计算出直径AD的长.从而得到⊙O的半径.
解答 解:作直径AD,连接CD,如图,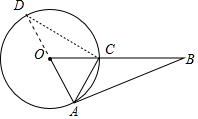
∵AD为直径,
∴∠ACD=90°,
∴∠D+∠DAC=90°,
∵BA与⊙O相切于点A,
∴OA⊥AB,
∴∠DAB=90°,即∠DAC+∠BAC=90°,
∴∠D=∠BAC,
∴tanD=tan∠BAC=$\frac{1}{2}$,
在Rt△ACD中,tanD=$\frac{AC}{CD}$,即$\frac{2}{CD}$=$\frac{1}{2}$,解得CD=4,
∴AD=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
∴⊙O的半径长为$\sqrt{5}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了正切的定义.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
16.下列命题中,真命题是( )
| A. | 有两边相等的平行四边形是菱形 | B. | 对角线垂直的四边形是菱形 | ||
| C. | 有一角为90°菱形是正方形 | D. | 对角线相等的四边形是矩形 |
17.2008年5月18日晚,中央电视台举办了“爱的奉献”大型募捐活动.据了解,本次活动社会各界共向四川灾区捐款大约1510000000元人民币,这个数字用科学记数法可表示为1.51×109元人民币.
14.下列说法正确的是( )
| A. | 将抛物线y=x2向左平移4个单位后,再向下平移2个单位,则此时抛物线的解析式是y=(x+4)2-2 | |
| B. | 方程x2+2x+3=0有两个不相等的实数根 | |
| C. | 平行四边形既是中心对称图形又是轴对称图形 | |
| D. | 平分弦的直径垂直于弦,并且平分这条弦所对的两条弧 |
18. 若函数y=kx-b的图象如图所示,则关于x的不等式k(x-3)-b>0的解集为( )
若函数y=kx-b的图象如图所示,则关于x的不等式k(x-3)-b>0的解集为( )
 若函数y=kx-b的图象如图所示,则关于x的不等式k(x-3)-b>0的解集为( )
若函数y=kx-b的图象如图所示,则关于x的不等式k(x-3)-b>0的解集为( )| A. | x<3 | B. | x>2 | C. | x<5 | D. | x>5 |
 如图,直线a∥b,∠1=85°,∠2=35°,则∠3为50°.
如图,直线a∥b,∠1=85°,∠2=35°,则∠3为50°.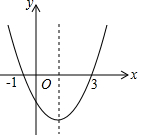 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列6个结论正确的有5个
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列6个结论正确的有5个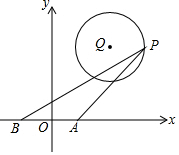 如图,在平面直角坐标系中,Q(3,4),P是在以Q为圆心,2为半径的⊙Q上一动点,A(1,0)、B(-1,0),连接PA、PB,则PA2+PB2的最小值是20.
如图,在平面直角坐标系中,Q(3,4),P是在以Q为圆心,2为半径的⊙Q上一动点,A(1,0)、B(-1,0),连接PA、PB,则PA2+PB2的最小值是20.