题目内容
5.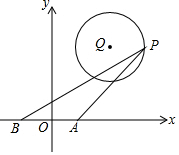 如图,在平面直角坐标系中,Q(3,4),P是在以Q为圆心,2为半径的⊙Q上一动点,A(1,0)、B(-1,0),连接PA、PB,则PA2+PB2的最小值是20.
如图,在平面直角坐标系中,Q(3,4),P是在以Q为圆心,2为半径的⊙Q上一动点,A(1,0)、B(-1,0),连接PA、PB,则PA2+PB2的最小值是20.
分析 设点P(x,y),表示出PA2+PB2的值,从而转化为求OP的最值,画出图形后可直观得出OP的最值,代入求解即可.
解答  解:设P(x,y),
解:设P(x,y),
∵PA2=(x+1)2+y2,PB2=(x-1)2+y2,
∴PA2+PB2=2x2+2y2+2=2(x2+y2)+2,
∵OP2=x2+y2,
∴PA2+PB2=2OP2+2,
当点P处于OQ与圆的交点上时,OP取得最值,
∴OP的最小值为OQ+PQ=5-2=3,
∴PA2+PB2最小值为20.
故答案为:20.
点评 本题考查了圆的综合,解答本题的关键是设出点P坐标,将所求代数式的值转化为求解OP的最小值,难度较大.

练习册系列答案
相关题目
7.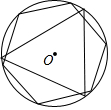 图中的正三角形和正六边形有公共的外接圆⊙O.则这个正三角形和正六边形边长的比为( )
图中的正三角形和正六边形有公共的外接圆⊙O.则这个正三角形和正六边形边长的比为( )
 图中的正三角形和正六边形有公共的外接圆⊙O.则这个正三角形和正六边形边长的比为( )
图中的正三角形和正六边形有公共的外接圆⊙O.则这个正三角形和正六边形边长的比为( )| A. | $\sqrt{6}$:2 | B. | $\sqrt{3}$:2 | C. | $\sqrt{3}$:1 | D. | 2:1 |
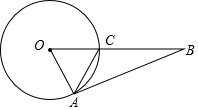 如图,OA,OC都是⊙O的半径,点B在OC的延长线上,BA与⊙O相切于点A,连接AC,若AC=2,tan∠BAC=$\frac{1}{2}$,则⊙O的半径长为$\sqrt{5}$.
如图,OA,OC都是⊙O的半径,点B在OC的延长线上,BA与⊙O相切于点A,连接AC,若AC=2,tan∠BAC=$\frac{1}{2}$,则⊙O的半径长为$\sqrt{5}$.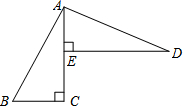 已知:如图,AC⊥BC于C,DE⊥AC于E,AD⊥AB于A,BC=AE.
已知:如图,AC⊥BC于C,DE⊥AC于E,AD⊥AB于A,BC=AE.