题目内容
18.阅读下列问题:$\frac{1}{{1+\sqrt{2}}}=\frac{{1×(\sqrt{2}-1)}}{{(\sqrt{2}+1)(\sqrt{2}-1)}}=\sqrt{2}-1$;
$\frac{1}{{\sqrt{3}+\sqrt{2}}}=\frac{{\sqrt{3}-\sqrt{2}}}{{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}}=\sqrt{3}-\sqrt{2}$;
$\frac{1}{{\sqrt{5}+2}}=\frac{{\sqrt{5}-2}}{{(\sqrt{5}+2)(\sqrt{5}-2)}}=\sqrt{5}-2$.
(1)求$\frac{1}{\sqrt{n+1}+\sqrt{n}}$(n为整数)的值.
(2)利用上面所揭示的规律计算:
$\frac{1}{1+\sqrt{2}}$+$\frac{1}{\sqrt{2}+\sqrt{3}}$+$\frac{1}{\sqrt{3}+\sqrt{4}}$+…+$\frac{1}{\sqrt{2010}+\sqrt{2011}}$+$\frac{1}{\sqrt{2011}+\sqrt{2012}}$.
分析 (1)根据平方差公式,可分母有理化;
(2)根据平方差公式,可分母有理化,根据实数的运算,可得答案.
解答 解:(1)$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\frac{\sqrt{n+1}-\sqrt{n}}{(\sqrt{n+1}+\sqrt{n})(\sqrt{n+1}-\sqrt{n})}$=$\sqrt{n+1}$-$\sqrt{n}$;
(2)原式=$\frac{\sqrt{2}-1}{(\sqrt{2}+1)(\sqrt{2}-1)}$+$\frac{\sqrt{3}-\sqrt{2}}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}$+$\frac{\sqrt{4}-\sqrt{3}}{(\sqrt{4}+\sqrt{3})(\sqrt{4}-\sqrt{3})}$+…+$\frac{\sqrt{2011}-\sqrt{2010}}{(\sqrt{2011}+\sqrt{2010})(\sqrt{2011}-\sqrt{2010})}$+$\frac{\sqrt{2012}-\sqrt{20111}}{(\sqrt{2012}+\sqrt{2011})(\sqrt{2012}-\sqrt{2011})}$
=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+…+$\sqrt{2011}$-$\sqrt{2010}$+$\sqrt{2012}$-$\sqrt{2011}$
=$\sqrt{2012}$-1
=2$\sqrt{503}$-1.
点评 本题考查了分母有理化,利用平方差公式分母有理化是解题关键.

练习册系列答案
相关题目

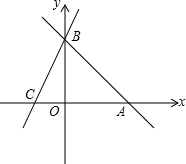 直线AB:y=-x+b分别与x,y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1.
直线AB:y=-x+b分别与x,y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1.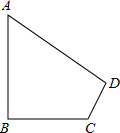 如图,在四边形ABCD中,∠A=60°,∠B=∠D=90°,BC=6,CD=4,求AB的长.
如图,在四边形ABCD中,∠A=60°,∠B=∠D=90°,BC=6,CD=4,求AB的长. 下面右边的图形是由8个棱长为1个单位的小立方体组成的立体图形,这个立体图形的主视图是( )
下面右边的图形是由8个棱长为1个单位的小立方体组成的立体图形,这个立体图形的主视图是( )


