Question

10．菱形的两条对角线长分别为18与24，则此菱形的周长为（　　）

• A． 15
• B． 30
• C． 60
• D． 120

Answer 1

分析 根据菱形的对角线互相垂直平分，可知AO和BO的长，再根据勾股定理即可求得AB的值，由菱形的四条边相等，继而求出菱形的周长．

解答 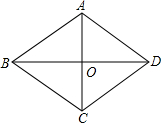解：∵AC=18，BD=24，菱形对角线互相垂直平分，
∴AO=9，BO=12cm，
∴AB=$\sqrt{{OB}^{2}+{OA}^{2}}$=$\sqrt{{12}^{2}+{9}^{2}}$=15，
∴菱形的周长=4×15=60．
故选C．

点评 本题考查的是菱形的性质，考查了菱形各边长相等的性质及勾股定理在直角三角形中的运用，根据勾股定理求AB的值是解题的关键．