Question

【题目】如图，在平面直角坐标系中，点，的坐标分别为和．是由经过一系列变化得到的．

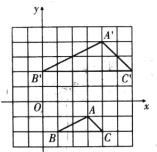
(1)请通过作图说明经过怎样的变化可以得到；

(2)若为内任一点，则它的对应点的坐标为 ．

Answer 1

【答案】(1)见解析；(2)

【解析】

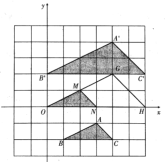
（1）先将向上平移2个单位，再向左平移1个单位，此时点和点重合，得到，再将以点为位似中心放大2倍，得到，将向上平移2个单位即可得到，由此作图即可；

（2）根据的平移规律是向上平移2个单位，再向左平移1个单位，通过位似放大2倍后再向上平移2个单位，由此即可得到点的坐标.

解：(1)先将向上平移2个单位，再向左平移1个单位，此时点和点重合，得到，再将以点为位似中心放大2倍，得到，将向上平移2个单位即可得到.

(2) 点P向上平移2个单位，再向左平移1个单位平移后的坐标为：（x-1，y+2），

通过位似变换得到的点坐标为：（2x-2，2y+4），

再向上平移2个单位，得到的点的坐标为，

故答案为：.