题目内容
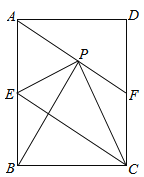
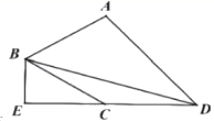
【题目】如图,四边形ABCD中,BD是对角线,![]() ,
,![]() ,
,![]() 交DC的延长线于E,若
交DC的延长线于E,若![]() ,
,![]() ,则AD的长为______.
,则AD的长为______.
【答案】![]()
【解析】
过A点向ED作垂线交于点F,过B点向AF作垂线交AF于点G,根据矩形的性质和勾股定理先把EF的长度求解出来,再次运用勾股定理即可得到答案.
如图,过A点向ED作垂线交于点F,过B点向AF作垂线交AF于点G,
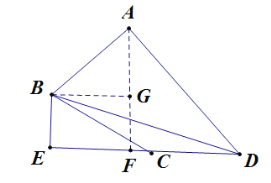
∵![]() 交DC的延长线于E,
交DC的延长线于E,
∴四边形BEFG是矩形(有三个角是90度的四边形是矩形),
∴GF=BE=1,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴直角三角形BCE中,∠ECB=30°,
∴EC=![]()
∴∠CDB=∠CBD=15°,
∴∠ADE=15°+30°=45°,
∴FD=AF,
假设EF=x,则BG=EF=x,
AG=![]() ,
,
∴在直角三角形ABG中,
![]() ,
,
∴![]() ,
,
即:![]()
解得:![]() ,或者
,或者![]() (舍去),
(舍去),
又∵EC=![]() ,
,
∴点F与点C重合,
∴AF=CD=2,
∴![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目