Question

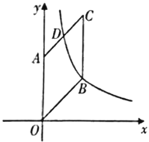
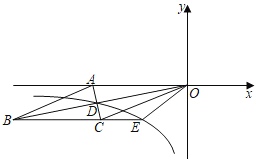
【题目】如图，菱形OABC的一边OA在x轴负半轴上．O是坐标原点，点A(﹣13，0)，对角线AC与OB相交于点D，且ACOB＝130，若反比例函数y＝（x＜0）的图象经过点D，并与BC的延长线交于点E．

（1）求双曲线y＝的解析式；

（2）求S△AOB：S△OCE之值．

Answer 1

【答案】（1）y＝；（2）52：23

【解析】

（1）△OAB与△OCE等高，若要求两者间的面积比只需求出底边的比，由AO＝10知需求CE的长，即求点E的坐标，需先求反比例函数解析式，而反比例函数解析式可先根据菱形的面积求得点D的坐标，据此求解可得；

（2）求得E的坐标，然后根据三角形面积公式求得△AOB和△OCE的面积，即可求得S△AOB：S△OCE之值．

解：（1）作CG⊥AO于点G，作BH⊥x轴于点H，

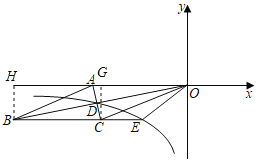
∵ACOB＝130，

∴S菱形OABC＝ACOB＝65，

∴S△OAC＝S菱形OABC＝，即AOCG＝，

∵A（﹣13，0），即OA＝13，

根据勾股定理得CG＝5，

在Rt△OGC中，∵OC＝OA＝13，

∴OG＝12，

则C（﹣12，﹣5），

∵四边形OABC是菱形，

∴AB∥OC，AB＝OC，

∴∠BAH＝∠COG，

在△BAH和△COG中

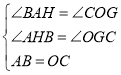
∴△BAH≌△COG（AAS），

∴BH＝CG＝5、AH＝OG＝12，

∴B（﹣25，5），

∵D为BO的中点，

∴D（﹣，﹣），

∵D在反比例函数图象上，

∴k＝﹣×（﹣）＝，即反比例函数解析式为y＝；

（2）当y＝﹣5时，x＝﹣，

则点E（﹣，﹣5），

∴CE＝，

∵S△OCE＝CECG＝××5＝，S△AOB＝AOBH＝×13×5＝，

∴S△AOB：S△OCE＝∶=52：23．