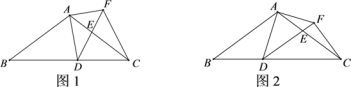题目内容
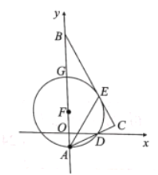
【题目】如图,![]() ,
,![]() 分别与
分别与![]() 相切于点
相切于点![]() 和点
和点![]() ,点
,点![]() 为弧
为弧![]() 上一点,连接
上一点,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,
,![]() 为弧
为弧![]() 上的一点,连接
上的一点,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,且
,且![]() .
.
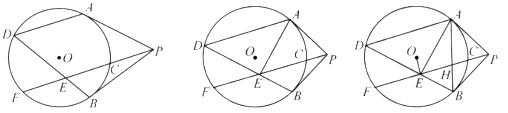
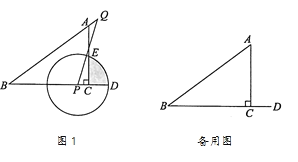
(1)如图1,求证:![]() ;
;
(2)如图2,连接![]() ,若
,若![]() ,求证:
,求证:![]() 平分
平分![]() ;
;
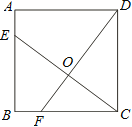
(3)如图3,在(2)的条件下,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)连接![]() 、
、![]() ,由切线的性质可得
,由切线的性质可得![]() ,由四边形内角和是
,由四边形内角和是![]() ,得
,得![]() ,由同弧所对的圆心角是圆周角的一半,得到
,由同弧所对的圆心角是圆周角的一半,得到![]() ,等量代换得到
,等量代换得到![]() ,由同位角相等两直线平行,得到
,由同位角相等两直线平行,得到![]() ;
;
(2)过点![]() 做
做![]() 交
交![]() 延长线于点
延长线于点![]() ,由
,由![]() 得
得![]() ,从而
,从而![]() ,由切线的性质,得
,由切线的性质,得![]() ,由
,由![]() ,
,![]() ,得
,得![]() ,从而
,从而![]() ,进而
,进而![]() ,即可证得
,即可证得![]() 由此
由此![]() ,得到
,得到![]() ,即可证得
,即可证得![]() 平分
平分![]() ;
;
(3)连接![]() 并延长交圆
并延长交圆![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,由
,由![]() ,
,![]() ,可得
,可得![]() ,由
,由![]() 、
、![]() 为半径,可得
为半径,可得![]() ,即可证出
,即可证出![]() ,由直径所对的圆周角是直角,可得
,由直径所对的圆周角是直角,可得![]() ,在
,在![]() 中,由正弦定义可得
中,由正弦定义可得![]() ,由此
,由此![]() ,由
,由![]() 为正方形,对角线
为正方形,对角线![]() 垂直平分
垂直平分![]() ,从而,
,从而,![]() .在
.在![]() 中,
中,![]() .延长
.延长![]() 交
交![]() 于
于![]() ,在
,在![]() 中,由勾股定理得
中,由勾股定理得![]() ,在
,在![]() 中,由勾股定理得
中,由勾股定理得![]() .
.
(1)连接![]() 、
、![]()
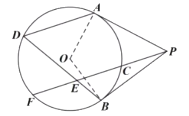
∵![]() 、
、![]() 与圆
与圆![]() 相切于点
相切于点![]() 、
、![]() ,且
,且![]() 、
、![]() 为半径,
为半径,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴在四边形![]() 中,
中,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]()
(2)过点![]() 做
做![]() 交
交![]() 延长线于点
延长线于点![]()
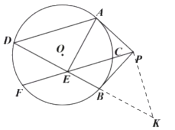
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 、
、![]() 为圆
为圆![]() 的切线,
的切线,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 平分
平分![]() ;
;
(3)连接![]() 并延长交圆
并延长交圆![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]()
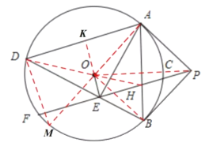
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() 、
、![]() 为半径,
为半径,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 为圆
为圆![]() 的直径,
的直径,
∴![]() ,
,
∵弧![]() 弧
弧![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,则
,则![]() ,
,
∴![]() ,
,
由题易证四边形![]() 为正方形,
为正方形,
∴对角线![]() 垂直平分
垂直平分![]() ,
,![]() ,
,
∵![]() 在
在![]() 上,
上,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
延长![]() 交
交![]() 于
于![]() ,
,
∵![]() ,可证
,可证![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]()
∴在![]() 中,
中,![]()
在![]() 中,
中,![]()
∵![]() ,
,![]()
∴![]()
∴![]() .
.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目