题目内容
3.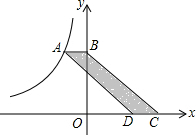 如图,在平面直角坐标系中,点A是函数y=$\frac{k}{x}$(k<0,x<0)图象上的点,过点A与y轴垂直的直线交y轴于点B,点C、D在x轴上,且BC∥AD.若四边形ABCD的面积为3,则k值为-3.
如图,在平面直角坐标系中,点A是函数y=$\frac{k}{x}$(k<0,x<0)图象上的点,过点A与y轴垂直的直线交y轴于点B,点C、D在x轴上,且BC∥AD.若四边形ABCD的面积为3,则k值为-3.
分析 根据已知条件得到四边形ABCD是平行四边形,于是得到四边形AEOB的面积=AB•OE,由于S平行四边形ABCD=AB•CD=3,得到四边形AEOB的面积=3,即可得到结论.
解答 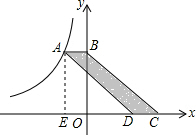 解:∵AB⊥y轴,
解:∵AB⊥y轴,
∴AB∥CD,
∵BC∥AD,
∴四边形ABCD是平行四边形,
∴四边形AEOB的面积=AB•OE,
∵S平行四边形ABCD=AB•CD=3,
∴四边形AEOB的面积=3,
∴|k|=3,
∵k<0,
∴k=-3,
故答案为:-3.
点评 本题考查了反比例函数系数k的几何意义,明确四边形AEOB的面积=S平行四边形ABCD是解题的关键.

练习册系列答案
相关题目
13.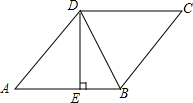 如图,在菱形ABCD中,DE⊥AB,cosA=$\frac{3}{5}$,BE=2,则tan∠DBE的值是( )
如图,在菱形ABCD中,DE⊥AB,cosA=$\frac{3}{5}$,BE=2,则tan∠DBE的值是( )
 如图,在菱形ABCD中,DE⊥AB,cosA=$\frac{3}{5}$,BE=2,则tan∠DBE的值是( )
如图,在菱形ABCD中,DE⊥AB,cosA=$\frac{3}{5}$,BE=2,则tan∠DBE的值是( )| A. | $\frac{1}{2}$ | B. | 2 | C. | 10$\sqrt{3}$ | D. | $\frac{\sqrt{5}}{5}$ |
8.比1小2的数是( )
| A. | -3 | B. | -2 | C. | -1 | D. | 0 |
13.若m>n,下列不等式一定成立的是( )
| A. | m-2>n+2 | B. | 2m>2n | C. | -$\frac{m}{2}$>$\frac{n}{2}$ | D. | m2>n2 |
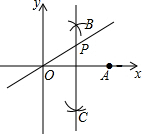 如图,在平面直角坐标系中,O为原点,点A的坐标为(4,0),分别以点O、A为圆心,大于OA一半的长为半径作圆弧,两弧交于点B、C,直线BC与直线y=$\frac{3}{4}$x交于点P,则点P的坐标为(2,$\frac{3}{2}$).
如图,在平面直角坐标系中,O为原点,点A的坐标为(4,0),分别以点O、A为圆心,大于OA一半的长为半径作圆弧,两弧交于点B、C,直线BC与直线y=$\frac{3}{4}$x交于点P,则点P的坐标为(2,$\frac{3}{2}$).
 如图,有3张不透明的卡片,除正面写有不同的数字外,其他均相同,将这3张卡片背面向上洗匀,从中随机抽取一张,记下数字后放回;重新洗匀后再从中随机抽取一张,将抽取的第一张、第二张卡片上的数字分别作为十位数字和个位数字组成两位数,请用画树状图(或列表)的方法,求这个两位数能被3整除的概率.
如图,有3张不透明的卡片,除正面写有不同的数字外,其他均相同,将这3张卡片背面向上洗匀,从中随机抽取一张,记下数字后放回;重新洗匀后再从中随机抽取一张,将抽取的第一张、第二张卡片上的数字分别作为十位数字和个位数字组成两位数,请用画树状图(或列表)的方法,求这个两位数能被3整除的概率.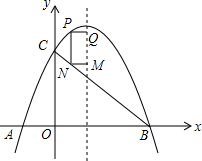 如图,平面直角坐标系中,抛物线y=ax2+bx+2与x轴分别交于点A(-1,0)、B(3,0),与y轴交于点C,连结BC.点P是BC上方抛物线上一点,过点P作y轴的平行线,交BC于点N,分别过P、N两点作x轴的平行线,交抛物线的对称轴于点Q、M,设P点的横坐标为m.
如图,平面直角坐标系中,抛物线y=ax2+bx+2与x轴分别交于点A(-1,0)、B(3,0),与y轴交于点C,连结BC.点P是BC上方抛物线上一点,过点P作y轴的平行线,交BC于点N,分别过P、N两点作x轴的平行线,交抛物线的对称轴于点Q、M,设P点的横坐标为m.