题目内容
17．
如图，AB是⊙O的直径，点C在AB的延长线上，CD切⊙O于点D，连接AD，若∠A=25°，请你求出∠C的度数．
分析 连接OD，由同弧所对的圆周角等于所对圆心角的一半求出∠DOB的度数，再由CD为圆的切线，利用切线的性质得到CD与OD垂直，即可确定出所求角的度数．
解答 
解：连接OD，
∵∠A=25°，
∴∠DOB=50°，
∵CD为⊙O的切线，
∴OD⊥CD，
∴∠C=90°-50°=40°．
点评 此题考查了切线的性质，以及圆周角定理，熟练掌握切线的性质是解本题的关键．
练习册系列答案
活力课时同步练习册系列答案
相关题目
7．如图，若AB∥CD，则α、β，γ之间的关系为（ ）
| A． | α+β+γ=360° | B． | α+β-γ=180° | C． | α+β+γ=180° | D． | α-β+γ=180° |
5．如果∠α=30°，那么∠α的余角是（ ）
| A． | 30° | B． | 150° | C． | 60° | D． | 70° |
如图，在△ABC中，∠ACB=90°，将△ABC绕点C，按顺时针方向旋转得△A1B1C，且A1B1∥BC，∠ABB1=30°，求旋转角∠BCB1的大小．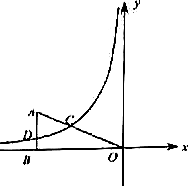
已知：在平面直角坐标系xOy中，过点A（-5，2）向x轴作垂线，垂足为B，连接AO，点C在线段AO上，且AC：CO=2：3，反比例函数y=$\frac{k}{x}$的图象经过点C，与边AB交于点D．
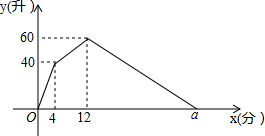某容器装有两个相同的注水管和一个出水管，注水管的注水速度和出水管的出水速度均为定值，从某一时刻开始，打开两个注水管向容器内注水4分钟，然后关闭一个注水管，打开出水管．出水管出水8分钟，关闭另一个注水管，容器内的水放完时关闭出水管．容器内的水量y（升）与时间x（分）之间的函数图象如图所示．