题目内容
11.长春市某校准备组织教师、学生、家长到大连进行参观学习活动,旅行社代办购买动车票,动车票价格如下表所示:| 运行区间 | 成人票价 | 学生票 | ||
| 出发站 | 终点站 | 一等座 | 二等座 | 二等座 |
| 长春 | 大连 | 65(元) | 54(元) | 40(元) |
(1)设参加活动的老师有m人,则教师和家长按照成人票价的一等座购买动车票的总费用是195m元(用含有m的代数式表示);
(2)设参加活动的学生有n人,求参加活动的老师、家长及学生分别有多少人?
(3)如果二等座动车票共买到x张,且学生全部按表中的“学生票二等座”购买,其余的买一等座动车票,且买票的总费用不低于9000元,直接写出x的最大值是193.
分析 (1)求出教师和家长的总人数,根据一等票和二等票两种情况求出代数式.
(2)设参加社会实践的老师有m人,学生有n人,则学生家长有2m人,根据若所有人员都买一等座的动车票,则共需13650元,若都买二等座动车票(学生全部按表中的“学生票二等座”购买),则共需8820元,可求出解.
(3)由(2)知所有参与人员总共有210人,其中学生有180人,所以买学生票共180张,有(x-180)名大人买二等座动车票,(210-x)名大人买一等座动车票,根据票的总费用不低于9000元,可列不等式求解.
解答 解:(1)购买一等票为:65•3m=195m;
故答案为:195m;
(2)根据题意得$\left\{\begin{array}{l}195m+65n=13650\\ 54×3m+40n=8820\end{array}\right.$;
解得:$\left\{\begin{array}{l}m=10\\ n=180\end{array}\right.$,
经检验,符合题意,则家长人数为2m=20.
答:参加活动的老师10人,家长20人,学生180人.
(3)由(2)知所有参与人员总共有210人,其中学生有180人,所以买学生票共180张,有(x-180)名大人买二等座动车票,(210-x)名大人买一等座动车票.
∴购 买 动 车 票 的 总 费 用 为40×180+54(x-180)+65(210-x)=-11x+11130
依题意,得:-11x+11130≥9000,
解得:$x≤193\frac{7}{11}$
经检验,符合题意
∵x为整数
∴x的最大值是193.
故答案为:193.
点评 本题考查理解题意的能力,关键是根据买一等票和二等票的价格做为等量关系求出人数,然后根据实际买票的总费用列出不等式求出解.

 阅读快车系列答案
阅读快车系列答案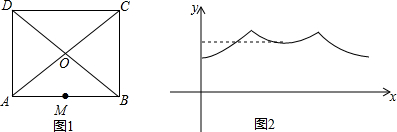
| A. | D→O→C | B. | A→D→C→B | C. | A→D→O→C→B | D. | O→D→C→O |
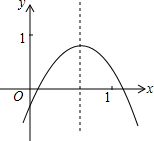 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的是( )| A. | a>0 | B. | abc>0 | C. | a+b+c<0 | D. | b2-4ac<0 |
| A. | (5,4) | B. | (-5,4) | C. | (5,-4) | D. | (-5,-4) |
 如图,△ABC中,AD⊥BC于D,E在BC上,F在BA延长线上,CE=2BD,EF=AC
如图,△ABC中,AD⊥BC于D,E在BC上,F在BA延长线上,CE=2BD,EF=AC