题目内容
 如图,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,CD=1,则AC=
如图,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,CD=1,则AC=考点:角平分线的性质,等腰直角三角形
专题:
分析:过点D作DE⊥AB于点E,由∠C=90°,AD是∠BAC的角平分线,DE⊥AB,根据角平分线的性质,即可得CD=DE,又由在△ABC中,AC=BC,∠C=90°,根据等腰三角形的性质,可求得AC=BC,∠B=45°,然后利用三角函数,即可求得AC的长.
解答: 解:过点D作DE⊥AB于点E,
解:过点D作DE⊥AB于点E,
∵∠C=90°,AD是∠BAC的角平分线,DE⊥AB,
∴DE=CD=1,
∵在△ABC中,AC=BC,∠C=90°,
∴∠CAB=∠B=45°,
∴∠EDB=∠B=45°,
∴sin∠B=sin45°=
=
=
,
∴BD=
=
∴AC=BC=CD+BD=1+
.
故答案为:1+
.
 解:过点D作DE⊥AB于点E,
解:过点D作DE⊥AB于点E,∵∠C=90°,AD是∠BAC的角平分线,DE⊥AB,
∴DE=CD=1,
∵在△ABC中,AC=BC,∠C=90°,
∴∠CAB=∠B=45°,
∴∠EDB=∠B=45°,
∴sin∠B=sin45°=
| DE |
| BD |
| 1 |
| BD |
| ||
| 2 |
∴BD=
| 2 | ||
|
| 2 |
∴AC=BC=CD+BD=1+
| 2 |
故答案为:1+
| 2 |
点评:本题考查的是角平分线的性质,熟知角的平分线上的点到角的两边的距离相等是解答此题的关键.

练习册系列答案
相关题目
 如图,直线y=x-1与反比例函数y=
如图,直线y=x-1与反比例函数y= 已知AB=6cm,AD=10cm,△ABE和△ADF的面积各是长方形ABCD面积的
已知AB=6cm,AD=10cm,△ABE和△ADF的面积各是长方形ABCD面积的 如图,△ABC的高BD、CE相交于点H,现给出四个判断:
如图,△ABC的高BD、CE相交于点H,现给出四个判断: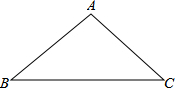 如图,在△ABC中,AB=AC=20,BC=32,点D在BC上,且AD=13,试确定点D的位置.
如图,在△ABC中,AB=AC=20,BC=32,点D在BC上,且AD=13,试确定点D的位置.