题目内容
设x1，x2，…，x20是正整数，且x1＜x2＜…＜x20，x1+x2+…+x20=1991，求x20的最小值．
考点：规律型：数字的变化类,有理数
专题：计算题,规律型
分析：设出最小的数x1，表示出其它数，代入x1+x2+…+x20=1991即可解决问题．
解答：解：假设x1+1=x2，x2+1=x3…
那么原式=20x1+（1+19）×20÷2=20x1+190=1991
所以x1=（1991-190）÷20=90.05，
如果取x1=91，则x20=110，（91+110）×20÷2=2010＞1991过大；
如果取x1=90，则x20=109，（90+109）×20÷2=1990＜1991；
所以x20的最小值是110．
那么原式=20x1+（1+19）×20÷2=20x1+190=1991
所以x1=（1991-190）÷20=90.05，
如果取x1=91，则x20=110，（91+110）×20÷2=2010＞1991过大；
如果取x1=90，则x20=109，（90+109）×20÷2=1990＜1991；
所以x20的最小值是110．
点评：此题利用假设的方法，逐步找出利用已知x1+x2+…+x20=1991解决问题．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
如图，一张长方形桌子可坐6人．那么将两张这样的桌子拼成一张大桌子后，最多可坐
下面所说的“平移”，是指只沿方格的格线（即上下或左右）运动，将图中的任一条线段平移1格称为“1步”．要通过平移，使图中的3条线段首尾相接组成一个三角形，最少需要移动（ ）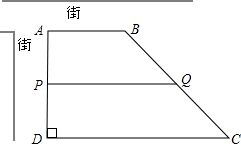
如图，现有一块梯形土地ABCD要出售，已测得上底AB=200m，高AD=230m，∠D=90°，∠C=45°．康宁房地产公司计划购买两面沿街的一块面积为25000m2的梯形地块ABQP，试求AP的长．