题目内容
1. 我国明代数学家程大位的名著《直指算法统宗》里有一道著名算题:
我国明代数学家程大位的名著《直指算法统宗》里有一道著名算题:一百馒头一百僧,大僧三个更无争,
小僧三人分一个,大小和尚各几丁?
如果译成白话文,其意思是:有100个和尚分100个馒头,
正好分完.如果大和尚一人分3个,小和尚3人分一个,试问大、小和尚各有几人?设大和尚x人,小和尚y人,可列方程组为$\left\{\begin{array}{l}{x+y=100}\\{3x+\frac{1}{3}y=100}\end{array}\right.$.
分析 根据100个和尚分100个馒头,正好分完.大和尚一人分3个,小和尚3人分一个得到等量关系为:大和尚的人数+小和尚的人数=100,大和尚分得的馒头数+小和尚分得的馒头数=100,依此列出方程组即可.
解答 解:设大和尚x人,小和尚y人,由题意可得
$\left\{\begin{array}{l}{x+y=100}\\{3x+\frac{1}{3}y=100}\end{array}\right.$.
故答案为$\left\{\begin{array}{l}{x+y=100}\\{3x+\frac{1}{3}y=100}\end{array}\right.$.
点评 本题考查了由实际问题抽象出二元一次方程组,关键以和尚数和馒头数作为等量关系列出方程组.

练习册系列答案
相关题目
11. 如图,将正六边形ABCDEF放置在直角坐标系内,A(-2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2016次翻转之后,点C的坐标是( )
如图,将正六边形ABCDEF放置在直角坐标系内,A(-2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2016次翻转之后,点C的坐标是( )
 如图,将正六边形ABCDEF放置在直角坐标系内,A(-2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2016次翻转之后,点C的坐标是( )
如图,将正六边形ABCDEF放置在直角坐标系内,A(-2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2016次翻转之后,点C的坐标是( )| A. | (4032,0) | B. | (4032,2$\sqrt{3}$) | C. | (4031,$\sqrt{3}$) | D. | (4033,$\sqrt{3}$) |
12. 如图,在空白网格内将某一个小正方形涂成阴影部分,且所涂的小正方形与原阴影图形的小正方形至少有一边重合.小红按要求涂了一个正方形,所得到的阴影图形恰好是轴对称图形的概率为( )
如图,在空白网格内将某一个小正方形涂成阴影部分,且所涂的小正方形与原阴影图形的小正方形至少有一边重合.小红按要求涂了一个正方形,所得到的阴影图形恰好是轴对称图形的概率为( )
 如图,在空白网格内将某一个小正方形涂成阴影部分,且所涂的小正方形与原阴影图形的小正方形至少有一边重合.小红按要求涂了一个正方形,所得到的阴影图形恰好是轴对称图形的概率为( )
如图,在空白网格内将某一个小正方形涂成阴影部分,且所涂的小正方形与原阴影图形的小正方形至少有一边重合.小红按要求涂了一个正方形,所得到的阴影图形恰好是轴对称图形的概率为( )| A. | $\frac{1}{5}$ | B. | $\frac{4}{15}$ | C. | $\frac{4}{9}$ | D. | $\frac{1}{3}$ |
6.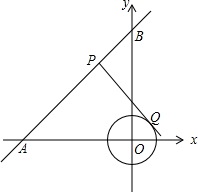 如图,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(-3,0)、B(0,4)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为( )
如图,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(-3,0)、B(0,4)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为( )
 如图,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(-3,0)、B(0,4)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为( )
如图,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(-3,0)、B(0,4)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为( )| A. | $\sqrt{7}$ | B. | $\frac{\sqrt{119}}{5}$ | C. | 2.4 | D. | 3 |
13.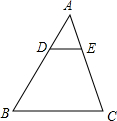 如图,在△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,则下列结论中正确的是( )
如图,在△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,则下列结论中正确的是( )
 如图,在△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,则下列结论中正确的是( )
如图,在△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,则下列结论中正确的是( )| A. | $\frac{AE}{AC}$=$\frac{1}{2}$ | B. | $\frac{DE}{BC}$=$\frac{1}{2}$ | ||
| C. | $\frac{△ADE的周长}{△ABC的周长}$=$\frac{1}{3}$ | D. | $\frac{△ADE的面积}{△ABC的面积}$=$\frac{1}{4}$ |
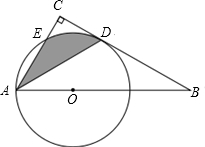 如图,Rt△ABC中,∠BAC=60°,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.
如图,Rt△ABC中,∠BAC=60°,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.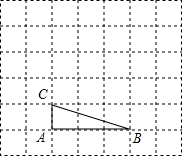 如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.
如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.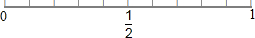 将下列事件发生的概率填在图中:(只填各事件的序号)
将下列事件发生的概率填在图中:(只填各事件的序号)