题目内容
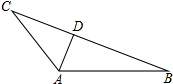 如图,
如图,| 1 |
| AD |
| 1 |
| AB |
| 1 |
| AC |
考点:平行线分线段成比例,等边三角形的判定与性质
专题:证明题
分析:延长CA到点E,使AE=AB,构造等边三角形,结合条件可得到
=
,证明△ADC∽△AEB,从而得到∠CAD=60°,可证得结论.
| BE |
| AD |
| AE |
| AC |
解答: 证明:
证明:
如图,延长CA至点E,使得AE=AB,连接BE,
∵∠BAC=120°,
∴∠BAE=60°,
∴△ABE为等边三角形,
∴AB=BE=AE,∠C=60°,
∴CE=AC+AE=AC+AB,
∵
=
+
=
=
,
∴
=
,
∴△ADC∽△AEB,
∴∠CAD=∠E=60°,
∴∠BAD=120°-60°=60°,
∴AD是∠BAC的角平分线.
 证明:
证明:如图,延长CA至点E,使得AE=AB,连接BE,
∵∠BAC=120°,
∴∠BAE=60°,
∴△ABE为等边三角形,
∴AB=BE=AE,∠C=60°,
∴CE=AC+AE=AC+AB,
∵
| 1 |
| AD |
| 1 |
| AB |
| 1 |
| AC |
| AB+AC |
| AB•AC |
| AE |
| BE•AC |
∴
| BE |
| AD |
| AE |
| AC |
∴△ADC∽△AEB,
∴∠CAD=∠E=60°,
∴∠BAD=120°-60°=60°,
∴AD是∠BAC的角平分线.
点评:本题主要考查等边三角形的判定和性质及相似三角形的判定和性质,构造等边三角形证明三角形相似从而得到∠CAD=60°是解题的关键.

练习册系列答案
相关题目
 如图,四边形ABCD,EFGH分别是⊙O的外切正四边形和内接正四边形,则
如图,四边形ABCD,EFGH分别是⊙O的外切正四边形和内接正四边形,则| EF |
| AB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列命题是真命题的是( )
| A、等底等高的两个三角形全等 |
| B、周长相等的直角三角形都全等 |
| C、有两边和一角对应相等的两个三角形全等 |
| D、有一边对应相等的两个等边三角形全等 |
已知a+b=10,a3+b3=100,ab等于( )
| A、10 | B、20 | C、30 | D、40 |
 如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC,CE⊥AD,垂足为O,EF∥BC.求证:EC平分∠FED.
如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC,CE⊥AD,垂足为O,EF∥BC.求证:EC平分∠FED.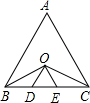 如图,在等边三角形ABC中,∠B、∠C的平分线交于O,过O作OD∥AB,OE∥AC,OD和OE分别交BC于点D、E.求证:BD=DE=EC.
如图,在等边三角形ABC中,∠B、∠C的平分线交于O,过O作OD∥AB,OE∥AC,OD和OE分别交BC于点D、E.求证:BD=DE=EC. 以A为顶点的射线个数,与直线l上的线段的条数有什么关系?为什么?
以A为顶点的射线个数,与直线l上的线段的条数有什么关系?为什么? 如图,Rt△ABC中,∠ACB=90°,AC=BC,点D、E分别为AB、BC的中点,AE与CD相交于点H,CF⊥AE交AB于点F,垂足为G,连结EF、FH和DG.
如图,Rt△ABC中,∠ACB=90°,AC=BC,点D、E分别为AB、BC的中点,AE与CD相交于点H,CF⊥AE交AB于点F,垂足为G,连结EF、FH和DG.