题目内容
 如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC,CE⊥AD,垂足为O,EF∥BC.求证:EC平分∠FED.
如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC,CE⊥AD,垂足为O,EF∥BC.求证:EC平分∠FED.考点:全等三角形的判定与性质,线段垂直平分线的性质
专题:证明题
分析:易证△AOE≌△AOC,可得AE=AC,即可证明△EAD≌△CAD,即可求得∠DEC=∠DCE,再根据平行线内错角相等可得∠DCE=∠DEF,即可解题.
解答:证明:在△AOE和△AOC中,
,
∴△AOE≌△AOC,(ASA)
∴AE=AC,
在△EAD和△CAD中,
,
∴△EAD≌△CAD,(SAS)
∴CD=DE,
∴∠DEC=∠DCE,
∵EF∥BC,
∴∠DCE=∠DEF,
∴∠CEF=∠DEC,
∴EC平分∠FED.
|
∴△AOE≌△AOC,(ASA)
∴AE=AC,
在△EAD和△CAD中,
|
∴△EAD≌△CAD,(SAS)
∴CD=DE,
∴∠DEC=∠DCE,
∵EF∥BC,
∴∠DCE=∠DEF,
∴∠CEF=∠DEC,
∴EC平分∠FED.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△EAD≌△CAD是解题的关键.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 如图,在△ABC中,AC=AB,∠BAC=90°,D是BC上的一动点,过点C作CE⊥BC,连接DE,求证:∠BAD=∠EDC.
如图,在△ABC中,AC=AB,∠BAC=90°,D是BC上的一动点,过点C作CE⊥BC,连接DE,求证:∠BAD=∠EDC. 如图所示,半径为1的圆O内切于一个圆心角为60°的扇形,圆O与扇形的半径和圆弧分别相切于点A,B,扇形所在的圆心为C,连接CB,求扇形的弧长.
如图所示,半径为1的圆O内切于一个圆心角为60°的扇形,圆O与扇形的半径和圆弧分别相切于点A,B,扇形所在的圆心为C,连接CB,求扇形的弧长. 如图,在△ABC中,AD平分∠BAC,DG⊥BC于点G,BG=CG,DE⊥AB于点E,DF⊥AC交AC的延长线于点F.求证:BE=CF.
如图,在△ABC中,AD平分∠BAC,DG⊥BC于点G,BG=CG,DE⊥AB于点E,DF⊥AC交AC的延长线于点F.求证:BE=CF. 如图,在四边形ABCD中,∠B=∠C=60°,点P在BC上,点E在DC上,且∠APE=∠B,
如图,在四边形ABCD中,∠B=∠C=60°,点P在BC上,点E在DC上,且∠APE=∠B,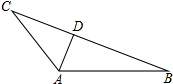 如图,
如图, 如图,△ABC中,∠ACB=90°,CD⊥AB于D,AC=5,BC=12,求CD的长.
如图,△ABC中,∠ACB=90°,CD⊥AB于D,AC=5,BC=12,求CD的长.