题目内容
 如图,Rt△ABC中,∠ACB=90°,AC=BC,点D、E分别为AB、BC的中点,AE与CD相交于点H,CF⊥AE交AB于点F,垂足为G,连结EF、FH和DG.
如图,Rt△ABC中,∠ACB=90°,AC=BC,点D、E分别为AB、BC的中点,AE与CD相交于点H,CF⊥AE交AB于点F,垂足为G,连结EF、FH和DG.①求证:△ACH≌△CBF;
②求证:AE=EF+FC;
③若AC=6,求线段DG的长.
考点:全等三角形的判定与性质
专题:
分析:(1)易证∠CAH=∠BCF,即可证明△ACH≌△CBF;
(2)易证∠HAD=∠FCD,即可证明△ADH≌△CDF,可得AH=CF,再可证明△CHE≌△BFE,可得HE=EF,即可解题;
(3)连接DE,过D作DM⊥AE于M,即可求得GE的长,再根据G,E分别是AB,BC中点,即可求得DE、EM、DM的长,即可解题.
(2)易证∠HAD=∠FCD,即可证明△ADH≌△CDF,可得AH=CF,再可证明△CHE≌△BFE,可得HE=EF,即可解题;
(3)连接DE,过D作DM⊥AE于M,即可求得GE的长,再根据G,E分别是AB,BC中点,即可求得DE、EM、DM的长,即可解题.
解答:解:(1)∵Rt△ABC中,∠ACB=90°,AC=BC,
∴△ABC是等腰直角三角形,
∵点D为AB的中点,
∴CD⊥AB.∠ACD=∠BCD=45°,
∵CF⊥AE,
∴∠CAH+∠AEC=∠BCF+∠AEC,
∴∠CAH=∠BCF,
在△ACH和△CBF中
∴△ACH≌△CBF(AAS);
(2)∵Rt△ABC中,∠ACB=90°,AC=BC,
∴△ABC是等腰直角三角形,
∵点D为AB的中点,
∴CD⊥AB.∠ACD=∠BCD=45°,
∴CD=AD,
∵CD⊥AB,CF⊥AE,
∴∠ADH=∠CGH,
∵∠AHD=∠CHG,
∴∠HAD=∠FCD,
在△ADH和△CDF中,
,
∴△ADH≌△CDF(AAS),
∴AH=CF,
∵△ACH≌△CBF,
∴CH=BF,
在△CHE和△BFE中,
,
∴△CHE≌△BFE(SAS),
∴HE=EF,
∴AH+HE=CF+EF,
即AE=EF+FC.
(3)连接DE,过D作DM⊥AE于M,

∴AE=
=3
,
∴CG=
=
,
GE=
,
∵G,E分别是AB,BC中点,
∴DE=3,DE∥AC,
∴∠DEM=∠CAE,
∴EM=
,DM=
,
∴MG=MD=
,
∴DG=
DM=
.
∴△ABC是等腰直角三角形,
∵点D为AB的中点,
∴CD⊥AB.∠ACD=∠BCD=45°,
∵CF⊥AE,
∴∠CAH+∠AEC=∠BCF+∠AEC,
∴∠CAH=∠BCF,
在△ACH和△CBF中
|
∴△ACH≌△CBF(AAS);
(2)∵Rt△ABC中,∠ACB=90°,AC=BC,
∴△ABC是等腰直角三角形,
∵点D为AB的中点,
∴CD⊥AB.∠ACD=∠BCD=45°,
∴CD=AD,
∵CD⊥AB,CF⊥AE,
∴∠ADH=∠CGH,
∵∠AHD=∠CHG,
∴∠HAD=∠FCD,
在△ADH和△CDF中,
|
∴△ADH≌△CDF(AAS),
∴AH=CF,
∵△ACH≌△CBF,
∴CH=BF,
在△CHE和△BFE中,
|
∴△CHE≌△BFE(SAS),
∴HE=EF,
∴AH+HE=CF+EF,
即AE=EF+FC.
(3)连接DE,过D作DM⊥AE于M,

∴AE=
| AC2+CE2 |
| 5 |
∴CG=
| AC•CE |
| AE |
6
| ||
| 5 |
GE=
3
| ||
| 5 |
∵G,E分别是AB,BC中点,
∴DE=3,DE∥AC,
∴∠DEM=∠CAE,
∴EM=
6
| ||
| 5 |
3
| ||
| 5 |
∴MG=MD=
3
| ||
| 5 |
∴DG=
| 2 |
3
| ||
| 5 |
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,考查了直角三角形中勾股定理的运用,本题中求证△ACH≌△CBF是解题的关键.

练习册系列答案
相关题目
 如图,在△ABC中,AD平分∠BAC,DG⊥BC于点G,BG=CG,DE⊥AB于点E,DF⊥AC交AC的延长线于点F.求证:BE=CF.
如图,在△ABC中,AD平分∠BAC,DG⊥BC于点G,BG=CG,DE⊥AB于点E,DF⊥AC交AC的延长线于点F.求证:BE=CF.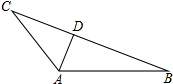 如图,
如图,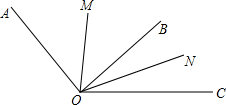 如图,设相邻两个角∠AOB,∠BOC的角平分线分别为OM,ON,如果∠MON=α(α为常数),那么∠AOC的度数是否为一个固定值?若是,请说明理由,并求出∠AOC的度数;若不是,请说明理由.
如图,设相邻两个角∠AOB,∠BOC的角平分线分别为OM,ON,如果∠MON=α(α为常数),那么∠AOC的度数是否为一个固定值?若是,请说明理由,并求出∠AOC的度数;若不是,请说明理由. 已知,如图,AB与CD相交于点O,AC∥DB,AO=BO,点E、F分别是OC、OD中点,求证:四边形ADBC是平行四边形.
已知,如图,AB与CD相交于点O,AC∥DB,AO=BO,点E、F分别是OC、OD中点,求证:四边形ADBC是平行四边形. 如图所示,是一个由小立方体搭成的几何体的俯视图,小正方体中数字表示该位置的小立方块的个数,则它的主视图为( )
如图所示,是一个由小立方体搭成的几何体的俯视图,小正方体中数字表示该位置的小立方块的个数,则它的主视图为( )



 如图,△ABC中,∠ACB=90°,CD⊥AB于D,AC=5,BC=12,求CD的长.
如图,△ABC中,∠ACB=90°,CD⊥AB于D,AC=5,BC=12,求CD的长. 如图,△ABC中,∠A=70°,DO,EO分别为AB,AC的垂直平分线,则∠BOC的度数是
如图,△ABC中,∠A=70°,DO,EO分别为AB,AC的垂直平分线,则∠BOC的度数是