题目内容
18.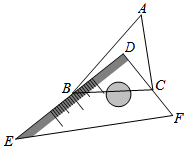 有一块直角三角板DEF放置在△ABC上,三角板DEF的两条直角边DE、DF恰好分别经过点B、C.△ABC中,∠A=50°,求∠DBA+∠DCA的度数.
有一块直角三角板DEF放置在△ABC上,三角板DEF的两条直角边DE、DF恰好分别经过点B、C.△ABC中,∠A=50°,求∠DBA+∠DCA的度数.
分析 先根据∠A=50°,得到∠ABC+∠ACB=180°-50°=130°,再根据∠D=90°,可得∠DBC+∠DCB=90°,最后根据∠DBA+∠DCA=(∠ABC+∠ACB)-(∠DBC+∠DCB)进行计算即可.
解答 解:∵∠A=50°,
∴∠ABC+∠ACB=180°-50°=130°,
而∠D=90°,
∴∠DBC+∠DCB=90°,
∴∠DBA+∠DCA=(∠ABC+∠ACB)-(∠DBC+∠DCB)
=130°-90°
=40°.
点评 本题考查了三角形内角和定理的运用,此题注意运用整体法计算,关键是求出∠ABC+∠ACB.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
13.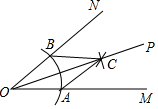 如图,用尺规作∠MON的平分线OP.由作图知△OAC≌△OBC,从而得OP平分∠MON,则此两个三角形全等的依据是( )
如图,用尺规作∠MON的平分线OP.由作图知△OAC≌△OBC,从而得OP平分∠MON,则此两个三角形全等的依据是( )
 如图,用尺规作∠MON的平分线OP.由作图知△OAC≌△OBC,从而得OP平分∠MON,则此两个三角形全等的依据是( )
如图,用尺规作∠MON的平分线OP.由作图知△OAC≌△OBC,从而得OP平分∠MON,则此两个三角形全等的依据是( )| A. | SAS | B. | ASA | C. | AAS | D. | SSS |
7. 如图,四边形ABD与四边形FGHE关于一个点成中心对称,则这个点是( )
如图,四边形ABD与四边形FGHE关于一个点成中心对称,则这个点是( )
 如图,四边形ABD与四边形FGHE关于一个点成中心对称,则这个点是( )
如图,四边形ABD与四边形FGHE关于一个点成中心对称,则这个点是( )| A. | O1 | B. | O2 | C. | O3 | D. | O4 |
8.抛物线y=(x-1)(x+3)顶点坐标是( )
| A. | (2,5) | B. | (-22,-3) | C. | (1,0) | D. | (-1,-4) |
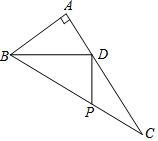 如图,在 Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,AB=4,BD=5,若点P是BC边上的动点,则线段DP的最小值为( )
如图,在 Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,AB=4,BD=5,若点P是BC边上的动点,则线段DP的最小值为( ) 如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,2),则关于x的不等式x+1>mx+n的解集为x>1.
如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,2),则关于x的不等式x+1>mx+n的解集为x>1. 如图,所示的几何体是由若干个大小相同的小正方体组成的,则该几何体的左视图(从左面看)是( )
如图,所示的几何体是由若干个大小相同的小正方体组成的,则该几何体的左视图(从左面看)是( )


