题目内容
7. 求证:两条平行直线被第三条直线所截,一对同旁内角的平分线互相垂直
求证:两条平行直线被第三条直线所截,一对同旁内角的平分线互相垂直解:如图,已知直线AB∥CD,直线OP,MN分别平分∠BOM,∠OMD,直线OP,MN交于G点.
求证:MN⊥OP
证明:∵AB∥CD(已知)
∴∠BOM+∠OMD=180°(两直线平行,同旁内角互补).
∵MN,OP分别平分∠OMD,∠BOM(已知),
∴2∠POM+2∠NMO=180°(角平分线的定义)
∴∠POM+∠PMO=90°(等式的性质)
∴∠MGO=90°(三角形的内角和定理)
∴MN⊥OP.
分析 两条平行直线被第三条直线所截,一对同旁内角的和是180°,然后根据角平分线的性质求出这对同旁内角和的一半是90°,即可求证一对同旁内角的平分线互相垂直.
解答  证明:∵AB∥CD(已知)
证明:∵AB∥CD(已知)
∴∠BOM+∠OMD=180°( 两直线平行,同旁内角互补).
∵MN,OP分别平分∠OMD,∠BOM(已知),
∴2∠POM+2∠NMO=180°(角平分线的定义)
∴∠POM+∠PMO=90°(等式的性质)
∴∠MGO=90°(三角形的内角和定理)
∴MN⊥OP.
故答案为:180°,两直线平行,同旁内角互补,180°,∠POM+∠PMO,∠MGO=90°
点评 本题主要考查了平行线的性质以及三角形内角和定理的运用,利用平行线的性质以及角平分线的性质,求证两直线相交所得的夹角是90°是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.下面关于绝对值的说法正确的是( )
| A. | 一个数的绝对值一定是正数 | |
| B. | 一个数的相反数的绝对值一定是正数 | |
| C. | 一个数的绝对值的相反数一定是负数 | |
| D. | 一个数的绝对值一定是非负数 |
2.一组数据1、2、3、0的极差是( )
| A. | 2 | B. | 3 | C. | 1 | D. | 3或-1 |
16.45的算术平方根在( )
| A. | 5和6之间 | B. | 6和7之间 | C. | 7和8之间 | D. | 8和9之间 |
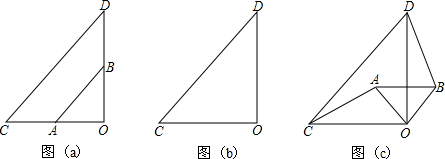
 如图所示,?ABCD中,G是BC延长线上的一点,AG与BD交于点E,与DC交于点F,此图中的相似三角形共有6对.
如图所示,?ABCD中,G是BC延长线上的一点,AG与BD交于点E,与DC交于点F,此图中的相似三角形共有6对.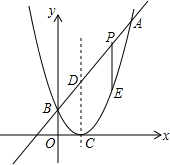 如图,己知二次函数图象的顶点坐标为C(1,0),直线y=x+m与该二次函数的图象交于A、B两点,与对称轴交于D(m,2),其中B点在y轴上
如图,己知二次函数图象的顶点坐标为C(1,0),直线y=x+m与该二次函数的图象交于A、B两点,与对称轴交于D(m,2),其中B点在y轴上