题目内容
2．
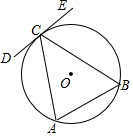如图，等腰三角形ABC内接于⊙O，BC=AC，过点C作DE∥AB，求证：DE为⊙O的切线．
分析 过C作CF垂直于AB，由三线合一性质得到F为AB中点，即CF垂直平分AB，由三角形外心在三角形边的垂直平分线上，得到CF过O，再由和平行线中一条垂直，与另一条也垂直得到DE与CF垂直，即可得证．
解答 
解：过C作CF⊥AB，
∵CA=CB，
∴F为AB中点，即CF垂直平分AB，
∴△ABC外心O在CF上，
∵DE∥AB，
∴FC⊥DE，
则DE为圆O的切线．
点评 此题考查了切线的判定，平行线的性质，以及等腰三角形三线合一性质，熟练掌握切线的判定方法是解本题的关键．
练习册系列答案
相关题目
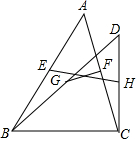如图，同底边BC的△ABC与△DBC中，E、F、G、H分别是AB、AC、DB、DC的中点，求证：EH与FG互相平分．
如图，已知AB∥CD，∠A=60°，∠C=25°，求∠E的度数．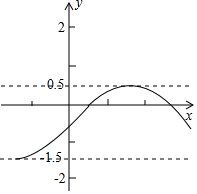
对于某一函数，给出如下定义：若存在实数M＞0，对于一函数任意的函数值y，都满足-M≤y≤M，则称这个函数是有界函数，在所有满足条件的M中，其最小值称为这个函数的确界值．例如如图所示的函数是有界函数，其确界值是1.5．问：将函数y=-x2（-m≤x≤1，m≥o）的图象向上平移m个单位，得到的函数的确界值是t，当m在什么范围时，满足$\frac{3}{4}≤t≤1$．
在一次高尔夫训练中，某球员从山坡下的点O打出一球，该球的飞行高度y（m）与飞行时间x（s）满足二次函数关系y=-$\frac{4}{27}$x2+bx，其函数图象如图所示，如果不考虑空气阻力，球的落点A距离点O的水平距离OB为12米时，垂直距离AB为$\frac{32}{3}$米．