题目内容
14.计算:(1)$\frac{{x}^{2}}{x-2}-\frac{4}{x-2}$
(2)($\frac{{a}^{2}-4}{{a}^{2}-4a+4}$-$\frac{1}{a-2}$)÷$\frac{a+1}{a+2}$
(3)$\frac{{x}^{2}-2x+1}{{x}^{3}-x}÷\frac{x-1}{{x}^{2}+x}$.
分析 结合分式的混合运算的概念和运算法则进行计算求解即可.
解答 解:(1)原式=$\frac{{x}^{2}-4}{x-2}$
=$\frac{(x-2)(x+2)}{x-2}$
=x+2.
(2)原式=($\frac{(a+2)(a-2)}{{(a-2)}^{2}}$-$\frac{1}{a-2}$)÷$\frac{a+1}{a+2}$
=$\frac{a+2-1}{a-2}$÷$\frac{a+1}{a+2}$
=$\frac{a+1}{a-2}$÷$\frac{a+1}{a+2}$
=$\frac{a+2}{a-2}$.
(3)原式=$\frac{{(x-1)}^{2}}{x{(x}^{2}-1)}$÷$\frac{x-1}{x(x+1)}$
=$\frac{(x-1)(x+1)}{{x}^{2}-1}$
=1.
点评 本题考查了分式的混合运算,解答本题的关键在于熟练掌握分式混合运算的概念和运算法则.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 如图,PA、PB是⊙O的切线,切点分别为A、B,∠APB=60°,⊙O的半径为2cm,则
如图,PA、PB是⊙O的切线,切点分别为A、B,∠APB=60°,⊙O的半径为2cm,则 如图,已知:∠1=∠2,∠D=60°,求∠B的度数.
如图,已知:∠1=∠2,∠D=60°,求∠B的度数.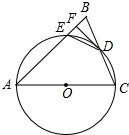 如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.
如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE. 如图,BD为⊙O的直径,AB=AC,AD交BC于E,AE=1,ED=2.
如图,BD为⊙O的直径,AB=AC,AD交BC于E,AE=1,ED=2.