题目内容
3. 如图,BD为⊙O的直径,AB=AC,AD交BC于E,AE=1,ED=2.
如图,BD为⊙O的直径,AB=AC,AD交BC于E,AE=1,ED=2.(1)求AB的长.
(2)延长DB到F,使得BF=BO,求证:直线FA与⊙O相切.
分析 (1)先证明△ABE∽△ADB,利用相似三角形的性质可求得AB的长;
(2)连接OA,在Rt△ABD中可求得BD,可证明△AOB为等腰三角形,结合BF=BO可证明∠OAF=90°,证得结论.
解答 (1)解:∵AB=AC,
∴∠ABC=∠ACB=∠ADB,∠BAE=∠DAB,
∴△ABE∽△ADB,
∴$\frac{AB}{AD}$=$\frac{AE}{AB}$,
∵AE=1,DE=2,
∴AD=AE+DE=3,
∴$\frac{AB}{3}$=$\frac{1}{AB}$,解得AB=$\sqrt{3}$;
(2)证明:如图,连接OA,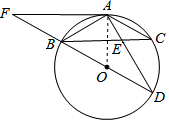
∵BD为直径,
∴△ABD为直角三角形,
在Rt△ABD中,AB=$\sqrt{3}$,AD=3,
∴BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=2$\sqrt{3}$,
∴AB=BO=AO,
∴∠BAO=60°,
∵BF=BO,
∴BF=AB,
∴∠BAF=∠F=$\frac{1}{2}$∠OBA=30°,
∴∠OAF=∠OAB+∠BAF=90°,
又∵∠ADB=∠AOB,
∴直线FA与⊙O相切.
点评 本题主要考查切线的判定及相似三角形的判定和性质的应用,掌握切线的判定方法是解题的关键,即有切点时连接圆心和切点,然后证明垂直,没有切点时,过圆心作垂直,证明圆心到直线的距离等于半径.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
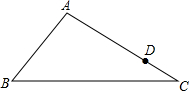 如图,在△ABC中,AB=3,BC=8,AC=6,点D在边AC上,且CD=4,过点D作一条直线交边AB于点E,使△ADE与△ABC相似,则DE的长是24.
如图,在△ABC中,AB=3,BC=8,AC=6,点D在边AC上,且CD=4,过点D作一条直线交边AB于点E,使△ADE与△ABC相似,则DE的长是24. 如图,已知AB是⊙O的直径,点C、D在⊙O上,且AB=5,BC=3.
如图,已知AB是⊙O的直径,点C、D在⊙O上,且AB=5,BC=3.
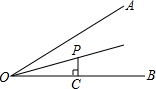 如图,∠AOB=30°,OP平分∠AOB,PC⊥OB于点C,若OC=1,则PC的长是2-$\sqrt{3}$.
如图,∠AOB=30°,OP平分∠AOB,PC⊥OB于点C,若OC=1,则PC的长是2-$\sqrt{3}$.