题目内容
1.解方程和不等式组(1)x2-3x=x-3
(2)$\left\{\begin{array}{l}{2x≥x-2}\\{\frac{2x+1}{3}>x}\end{array}\right.$.
分析 (1)移项后分解因式,即可得出两个方程,求出方程的解即可;
(2)先求出每个不等式的解集,再根据找不等式组解集的规律找出不等式组的解集即可.
解答 解:(1)x2-3x=x-3,
x(x-3)-(x-3)=0,
(x-3)(x-1)=0,
x-3=0,x-1=0,
x1=3,x2=1;
(2)$\left\{\begin{array}{l}{2x≥x-2①}\\{\frac{2x+1}{3}>x②}\end{array}\right.$
∵解不等式①得:x≥-2,
解不等式②得:x<1,
∴原不等式组的解集是-2≤x<1.
点评 本题考查了解一元一次不等式组,解一元二次方程的应用,能把二元一次方程组转化成一元一次方程是解(1)的关键,能根据不等式的解集找出不等式组的解集是解(2)的关键.

练习册系列答案
相关题目
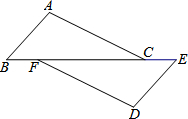 已知:如图,点B、F、C、E在一条直线上,BF=CE,AC=DF,且AC∥DF.
已知:如图,点B、F、C、E在一条直线上,BF=CE,AC=DF,且AC∥DF.



 如图,在边长为12的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G.则BG的长为( )
如图,在边长为12的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G.则BG的长为( )