题目内容
6.先化简,再求值.$\frac{{2{x^2}+6x}}{{{x^2}-4x+4}}$•$\frac{x-2}{{{x^2}+3x}}-\frac{1}{{\sqrt{{x^2}-4x+4}}}$,其中x=2-$\sqrt{2}$.分析 先根据x的值判断出x-2的符号,再由分式混合运算的法则把原式进行化简,把x的值代入进行计算即可.
解答 解:∵x=2-$\sqrt{2}$,
∴x-2=-$\sqrt{2}$<0
原式=$\frac{2x(x+3)}{(x-2)^{2}}$•$\frac{x-2}{x(x+3)}$-$\frac{1}{2-x}$
=$\frac{2}{x-2}$+$\frac{1}{x-2}$
=$\frac{3}{x-2}$,
当x=2-$\sqrt{2}$时,原式=$\frac{3}{-\sqrt{2}}$=-$\frac{3\sqrt{2}}{2}$.
点评 本题考查的是分式的化简求值,先根据题意判断出x-2的符号是解答此题的关键.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
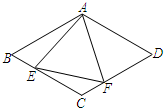 如图,菱形ABCD中,AB=4,∠B=60°,E,F分别是BC,DC上的点,∠EAF=
如图,菱形ABCD中,AB=4,∠B=60°,E,F分别是BC,DC上的点,∠EAF= 在△ABC中,AB=10cm,AC=8cm,边BC的垂直平分线分别交AB,BC于点E,D,求△ACE的周长.
在△ABC中,AB=10cm,AC=8cm,边BC的垂直平分线分别交AB,BC于点E,D,求△ACE的周长.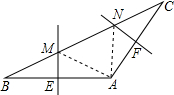 在△ABC中,AB的垂直平分线交BC于M,交AB于E,AC的垂直平分线交BC于N,交AC于F.
在△ABC中,AB的垂直平分线交BC于M,交AB于E,AC的垂直平分线交BC于N,交AC于F.