题目内容
5.一条弦把圆分成1:3两部分,则劣弧所对的圆心角为90°,圆周角为45°或135°.分析 先根据圆心角、弧、弦的关系求出劣弧所对圆心角的度数,再根据圆周角定理得出该弦所对圆周角的度数即可.
解答 解:∵一条弦把圆周分成1:3的两段弧,
∴劣弧所对圆心角的度数=$\frac{1}{4}$×360°=90°,优弧所对圆心角的度数=$\frac{3}{4}$×360°=270°;
∴弦所对的圆周角的度数=$\frac{1}{2}$×90°=45°和$\frac{1}{2}$×270°=135°.
故答案为:90°;45°和135°
点评 本题考查的是圆心角、弧、弦的关系及圆周角定理,在解答此类问题时要注意是在“同圆或等圆中”才适用,这是此类问题的易错点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.无论a取何值,下列各式中一定有意义的是( )
| A. | $\sqrt{a+1}$ | B. | $\sqrt{{a^2}-1}$ | C. | a-2 | D. | $\sqrt{{a^2}+1}$ |
14.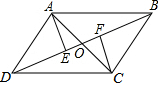 如图,已知AB∥CD,AD∥BC,AC与BD交于点O,AE⊥BD于点E,CF⊥BD于点F,那么图中全等的三角形有( )
如图,已知AB∥CD,AD∥BC,AC与BD交于点O,AE⊥BD于点E,CF⊥BD于点F,那么图中全等的三角形有( )
 如图,已知AB∥CD,AD∥BC,AC与BD交于点O,AE⊥BD于点E,CF⊥BD于点F,那么图中全等的三角形有( )
如图,已知AB∥CD,AD∥BC,AC与BD交于点O,AE⊥BD于点E,CF⊥BD于点F,那么图中全等的三角形有( )| A. | 5对 | B. | 6对 | C. | 7对 | D. | 8对 |
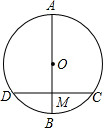 如图,⊙O的直径AB垂直弦CD于M,且M是半径OB的中点,CD=8cm,求直径AB的长.
如图,⊙O的直径AB垂直弦CD于M,且M是半径OB的中点,CD=8cm,求直径AB的长. 如图,已知△ABF≌△DCE,BE、FC在同一直线上,BE=2cm,求CF的长.
如图,已知△ABF≌△DCE,BE、FC在同一直线上,BE=2cm,求CF的长.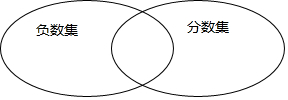 如图,两个圈分别表示负数集和分数集,请将3,0,$\frac{1}{2}$,-3$\frac{1}{3}$,-5,-3.4中符合条件的数填入圈中.
如图,两个圈分别表示负数集和分数集,请将3,0,$\frac{1}{2}$,-3$\frac{1}{3}$,-5,-3.4中符合条件的数填入圈中.