题目内容
13.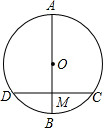 如图,⊙O的直径AB垂直弦CD于M,且M是半径OB的中点,CD=8cm,求直径AB的长.
如图,⊙O的直径AB垂直弦CD于M,且M是半径OB的中点,CD=8cm,求直径AB的长.
分析 连接OC,根据垂径定理可求CM=DM=4cm,再运用勾股定理可求半径OC,则直径AB可求.
解答  解:连接OC,
解:连接OC,
∵直径AB⊥CD,
∴CM=DM=$\frac{1}{2}$CD=4cm,
设圆的半径是r,
∵M是OB的中点,
∴OM=$\frac{1}{2}$r,
由勾股定理得:
OC2=OM2+CM2
∴r2=($\frac{1}{2}$r)2+42,
解得:r=$\frac{8\sqrt{3}}{3}$,
则直径AB=2r=$\frac{16\sqrt{3}}{3}$(cm).
点评 本题考查了垂径定理,解此类题一般要把半径、弦心距、弦的一半构建在一个直角三角形里,运用勾股定理求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.下列三角形中,一定是直角三角形的有( )
①有两个内角互余的三角形
②三边长为m2-n2,2mn,m2+n2(m>n>0)的三角形
③三边之比为3:4:5的三角形
④三个内角的比是1:2:3的三角形.
①有两个内角互余的三角形
②三边长为m2-n2,2mn,m2+n2(m>n>0)的三角形
③三边之比为3:4:5的三角形
④三个内角的比是1:2:3的三角形.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.已知$\frac{1}{5}$a=$\frac{2}{3}$b,那么a:b=( )
| A. | 10:3 | B. | 3:10 | C. | 2:15 | D. | 15:2 |
 如图,D是△ABC中边BC的中点,∠ABD=∠ACD,且AB=AC.求证:
如图,D是△ABC中边BC的中点,∠ABD=∠ACD,且AB=AC.求证: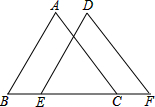 如图,已知∠B=∠DEF,AB=DE,要证明△ABC≌△DEF.
如图,已知∠B=∠DEF,AB=DE,要证明△ABC≌△DEF.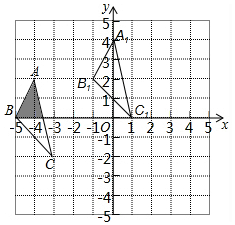 如图,方格纸中的每个小方格都是边长为1个单位的正方形,已知△ABC的顶点均在格点上,建立直角坐标系后,点B的坐标为(-5,0)
如图,方格纸中的每个小方格都是边长为1个单位的正方形,已知△ABC的顶点均在格点上,建立直角坐标系后,点B的坐标为(-5,0)