题目内容
6.(1)已知抛物线y=x2-4x+3与x轴的交点分别为A、B,求AB的长;(2)已知抛物线y=x2-4x+m-2与x轴的交点分别为A、B,且AB=6,求m的值.
分析 (1)当y=0时,代入解方程求出方程的解,并计算AB=|x1-x2|的长;
(2)先设A、B两点的坐标,由根与系数的关系代入等式AB=6中,得到关于m的方程,解出即可.
解答 解:(1)当y=0时,x2-4x+3=0,
(x-3)(x-1)=0,
x1=3,x2=1,
∴AB=3-1=2,
(2)设A(x1,0),B(x2,0),
当y=0时,x2-4x+m-2=0,
则x1+x2=4,x2•x1=m-2,
∵AB=6,
∴|x1-x2|=6,
(x1-x2)2=36,
${{x}_{1}}^{2}$-2x1x2+${{x}_{2}}^{2}$=36,
(x1+x2)2-4x1x2=36,
42-4(m-2)=36,
m=-3.
点评 本题考查了抛物线与x轴的交点,即令y=0,得到一元二次方程,解出即可;同时两交点的距离AB=|x1-x2|;掌握根与系数的关系,会利用完全平方公式进行变形.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
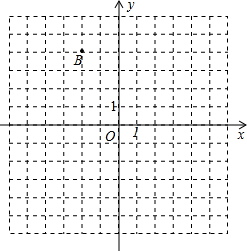 如图在直角坐标平面内,已知点A(-2,-3)与点B,将点A向右平移7个单位到达点C.
如图在直角坐标平面内,已知点A(-2,-3)与点B,将点A向右平移7个单位到达点C.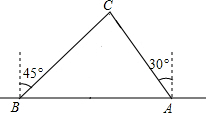 为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度,一天,我国两艘海监船刚好在某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域,如图,在B处测得C在东北方向上,在A处测得C在北偏西30°的方向上.
为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度,一天,我国两艘海监船刚好在某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域,如图,在B处测得C在东北方向上,在A处测得C在北偏西30°的方向上.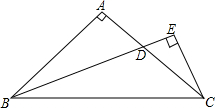 如图,在△ABC中,∠A=90°,AB=AC,∠ABC的平分线BD交AC于点D,CE⊥BD,垂足为点E,以试猜想CE与BD的数量关系,并说明理由.
如图,在△ABC中,∠A=90°,AB=AC,∠ABC的平分线BD交AC于点D,CE⊥BD,垂足为点E,以试猜想CE与BD的数量关系,并说明理由.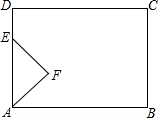 如图,在矩形ABCD中,AB=8cm,BC=6cm,动点E从点A出发.以2cm/s的速度沿射线AD方向运动,以AE为底边,在AD的右侧作等腰直角角形AEF,当点F落在射线BC上时,点E停止运动,设△AEF与矩形ABCD重叠部分的面积为S,运动的时间为t(s).
如图,在矩形ABCD中,AB=8cm,BC=6cm,动点E从点A出发.以2cm/s的速度沿射线AD方向运动,以AE为底边,在AD的右侧作等腰直角角形AEF,当点F落在射线BC上时,点E停止运动,设△AEF与矩形ABCD重叠部分的面积为S,运动的时间为t(s).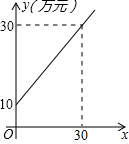 生产某种产品所需的成本y(万元)与数量x(t)之间的关系如图所示.
生产某种产品所需的成本y(万元)与数量x(t)之间的关系如图所示. 如图,已知在△ABC中,AB=AC,BD⊥AC,AE⊥BC.求证:∠DBC=$\frac{1}{2}$∠BAC.
如图,已知在△ABC中,AB=AC,BD⊥AC,AE⊥BC.求证:∠DBC=$\frac{1}{2}$∠BAC.