Question

11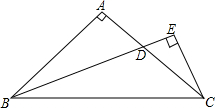．如图，在△ABC中，∠A=90°，AB=AC，∠ABC的平分线BD交AC于点D，CE⊥BD，垂足为点E，以试猜想CE与BD的数量关系，并说明理由．

Answer 1

分析 延长BA、CE相交于点F，利用“角边角”证明△BCE和△BFE全等，根据全等三角形对应边相等可得CE=EF，根据等角的余角相等求出∠ABD=∠ACF，然后利用“角边角”证明△ABD和△ACF全等，根据全等三角形对应边相等可得BD=CF，然后求解即可．

解答 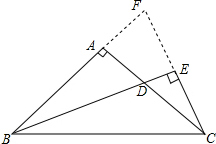解：BD=2CE．
理由如下：如图，延长BA、CE相交于点F，
∵BD平分∠ABC，
∴∠ABD=∠CBD，
在△BCE和△BFE中，$\left\{\begin{array}{l}{∠ABD=∠CBD}\\{BE=BE}\\{∠BEF=∠BEC=90°}\end{array}\right.$，
∴△BCE≌△BFE（ASA），
∴CE=EF，
∵∠A=90°，CE⊥BD，
∴∠ACF+∠F=90°，∠ABD+∠F=90°，
∴∠ABD=∠ACF，
在△ABD和△ACF中，$\left\{\begin{array}{l}{∠ABD=∠ACF}\\{AB=AC}\\{∠BAC=∠CAF=90°}\end{array}\right.$，
∴△ABD≌△ACF（ASA），
∴BD=CF，
∵CF=CE+EF=2CE，
∴BD=2CE．

点评 本题考查了全等三角形的判定与性质，等角的余角相等的性质，熟练掌握三角形全等的判定方法是解题的关键，难点在于作辅助线构造出全等三角形并得到与BD相等的线段CF．