题目内容
16. 如图,已知在△ABC中,AB=AC,BD⊥AC,AE⊥BC.求证:∠DBC=$\frac{1}{2}$∠BAC.
如图,已知在△ABC中,AB=AC,BD⊥AC,AE⊥BC.求证:∠DBC=$\frac{1}{2}$∠BAC.
分析 根据同角的余角相等求出∠DBC=∠CAE,再根据等腰三角形三线合一的性质可得∠CAE=$\frac{1}{2}$BAC,从而得证.
解答 证明:∵BD⊥AC,AE⊥BC,
∴∠DBC+∠C=90°,
∠CAE+∠C=90°,
∴∠DBC=∠CAE,
∵AB=AC,AE⊥BC.
∴∠CAE=$\frac{1}{2}$BAC(等腰三角形三线合一),
∴∠DBC=$\frac{1}{2}$∠BAC.
点评 本题考查了等腰三角形三线合一的性质,同角的余角相等的性质,熟记性质并准确识图是解题的关键.

练习册系列答案
相关题目
8.将(3x+2)-2(2x-1)去括号正确的是( )
| A. | 3x+2-2x+1 | B. | 3x+2-4x+1 | C. | 3x+2-4x-2 | D. | 3x+2-4x+2 |
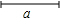 已知线段a,求作,△ABC,使AB=a,AC=BC=2a,画出图形后,测量一下∠CAB与∠CBA,猜想∠CAB与∠CBA的关系,你能说明你发现的结论吗?
已知线段a,求作,△ABC,使AB=a,AC=BC=2a,画出图形后,测量一下∠CAB与∠CBA,猜想∠CAB与∠CBA的关系,你能说明你发现的结论吗? 如图,在△ABC中,∠ACB=90°,CD是∠ACB的平分线,将△ABC绕点C按逆时针方向旋转,边AC落在直线CD上,得到△A1B1C1,A1B1交边BC于F.求证:CF+A1D=AC.
如图,在△ABC中,∠ACB=90°,CD是∠ACB的平分线,将△ABC绕点C按逆时针方向旋转,边AC落在直线CD上,得到△A1B1C1,A1B1交边BC于F.求证:CF+A1D=AC. 如图:矩形ABCD的对角线相交于点O,AB=5cm,∠AOB=60°,则AD=5$\sqrt{3}$cm.
如图:矩形ABCD的对角线相交于点O,AB=5cm,∠AOB=60°,则AD=5$\sqrt{3}$cm.