题目内容
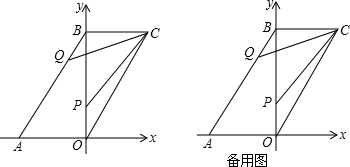
2.如图,四边形OABC是平行四边形,点A(-2,0),点B(0,2$\sqrt{3}$),动点P从点O出发以每秒$\sqrt{3}$个单位长度的速度沿射线OB方向匀速运动,同时动点Q从点B出发以每秒2个单位长度的速度沿射线BA方向匀速运动,连结CP,CQ,设运动时间为t秒.(1)求点C的坐标和∠OCB的度数;
(2)请用含t的代数式表示动点P和动点Q的坐标;
(3)①当∠BCP=∠BCQ时,求t的值;
②当∠BCQ-∠BCP≤30°时,求t的取值范围(只要写出直接答案).
分析 (1)由平行四边形的性质和点A、B的坐标便可求出C点坐标,根据直角三角形的边角关系可知∠OCB的度数;
(2)利用三角形相似可求出点Q的坐标,点P在y轴上,易得P(0,t);
(3)①当∠BCP=∠BCQ时,点Q在直线CP上,求出直线CP的解析式,把Q的坐标代入列方程求解;
②运用C、Q的坐标求出直线CQ的解析式,求出直线与y轴交点D的坐标,表示出OP、DP、CP,运用相似列方程求解,得到t的取值范围.
解答 解:(1)∵四边形OABC是平行四边形,点A(-2,0),点B(0,2$\sqrt{3}$),
∴C(2,2$\sqrt{3}$)
在Rt△OBC中,OB=2$\sqrt{3}$,BC=2,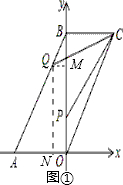
∴∠∠OCB=30°
(2)∵动点P从点O出发以每秒$\sqrt{3}$个单位长度的速度沿射线OB方向匀速运动,运动时间为t秒.
∴P(0,$\sqrt{3}$t,)
如图①,作QM⊥y,QN⊥x,
则$\frac{QM}{OA}$=$\frac{BQ}{AB}$,$\frac{QN}{OB}$=$\frac{AQ}{AB}$,
由BQ=2t,AB=4,OB=2$\sqrt{3}$,OA=2,
∴AQ=4-2t,
代入上式解得:QM=t,QN=2$\sqrt{3}$-$\sqrt{3}$t,
∴Q(-t,2$\sqrt{3}$-$\sqrt{3}$t),P(0,$\sqrt{3}$t);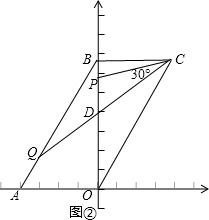
(3)①当∠BCP=∠BCQ时,点Q在直线CP上,
设直线CP解析式为y=kx+b,
代入C、P两点坐标,得
k=$\frac{2\sqrt{3}-\sqrt{3}t}{2}$,b=$\sqrt{3}$t,
∴y=$\frac{2\sqrt{3}-\sqrt{3}t}{2}$x+$\sqrt{3}$t,
把Q(-t,2$\sqrt{3}$-$\sqrt{3}$t)代入解方程得:t=-1$±\sqrt{5}$,
t=-1-$\sqrt{5}$不合题意,舍去,
∴t=$\sqrt{5}$-1.②
②如图②当∠BCQ-∠BCP=30°时,
∵∠PCD=∠COB=30°,∠CPO=∠DPC,
∴△OCP∽△CDP,
∴PC2=PD•PO,
∵Q(-t,2$\sqrt{3}$-$\sqrt{3}$t),C(2,2$\sqrt{3}$),
设直线CQ的解析式为y=kx+b,
把C、Q两点坐标代入得:k=-$\frac{\sqrt{3}t}{t-2}$,b=$\frac{4\sqrt{3}t-4\sqrt{3}}{t-2}$,
∴D(0,$\frac{4\sqrt{3}t-4\sqrt{3}}{t-2}$),
∴OP=$\sqrt{3}$t,PD=$\sqrt{3}$t-$\frac{4\sqrt{3}t-4\sqrt{3}}{t-2}$,PC2=BP2+BC2=(2$\sqrt{3}$-$\sqrt{3}$t)2+22
∴(2$\sqrt{3}$-$\sqrt{3}$t)2+22=$\sqrt{3}$t•($\sqrt{3}$t-$\frac{4\sqrt{3}t-4\sqrt{3}}{t-2}$)
解得t=$\frac{8}{7}$,
∴0<t≤$\frac{8}{7}$.
点评 本题考查了相似三角形的判定与性质、平行四边形的性质及待定系数法;熟练运用数形结合是解决此类问题的关键.

| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{1}{3}$ | D. | 3 |
| A. | 2 | B. | -2 | C. | -$\frac{1}{2}$ | D. | ±2 |
| A. | (3,4)或(-3,-4) | B. | (-3,-4)或(3,-4)或(-3,4)或(3,4) | ||
| C. | (4,3)或(-4,-3) | D. | (4,3)或(4,-3)或(-4,3)或(-4,-3) |
| A. | 32,42,52 | B. | $1,\sqrt{2},\sqrt{3}$ | C. | $1,2,\sqrt{3}$ | D. | $1,\sqrt{2},1$ |

 如图,点A、C的坐标分别为(3,0)、(0,2),分别过点A,C作x轴、y轴的垂线交于点B.
如图,点A、C的坐标分别为(3,0)、(0,2),分别过点A,C作x轴、y轴的垂线交于点B.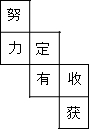 水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示,如图是一个正方体的表面展开图,若图中“定”在正方体的前面,那么这个正方体的后面是( )
水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示,如图是一个正方体的表面展开图,若图中“定”在正方体的前面,那么这个正方体的后面是( )