题目内容
如果要使关于x的方程
-2m+1=
有唯一解，那么m的取值范围为 ．
| x |
| x-3 |
| m |
| x-3 |
考点：分式方程的解
专题：
分析：分式方程去分母转化为整式方程，根据分式方程有唯一解得到2-2m≠0，分式有意义的条件可得3（2-2m）≠3-5m，解不等式即可得到m的取值范围．
解答：解：分式方程去分母得：x-2m（x-3）+（x-3）=m，
整理得（2-2m）x=3-5m，
由分式方程有唯一解得到2-2m≠0，即m≠1，
由分式有意义的条件可得3（2-2m）≠3-5m，解得m≠3．
故答案为：m≠1或m≠3．
整理得（2-2m）x=3-5m，
由分式方程有唯一解得到2-2m≠0，即m≠1，
由分式有意义的条件可得3（2-2m）≠3-5m，解得m≠3．
故答案为：m≠1或m≠3．
点评：本题考查了分式方程的解，解不等式，此题难度适中．
练习册系列答案
浙江之星课时优化作业系列答案
激活思维优加课堂系列答案
相关题目
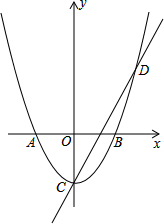如图，在平面直角坐标系中，抛物线与x轴交于点A（-1，0）和点B（1，0），直线y=2x-1与y轴交于点C，与抛物线交于点C、D．
如图，PA为⊙O的切线，A为切点，直线PO平分弦AB交AB于点D，交⊙O于点E、F，
如图，直线y=2x+4与x，y轴分别交于A，B两点，以OB为边在y轴右侧作等边三角形OBC，将点C向左平移，使其对应点C′恰好落在直线AB上，则点C′的坐标为