题目内容
 如图,PA为⊙O的切线,A为切点,直线PO平分弦AB交AB于点D,交⊙O于点E、F,
如图,PA为⊙O的切线,A为切点,直线PO平分弦AB交AB于点D,交⊙O于点E、F,(1)试判断直线PB与⊙O的位置关系,并说明理由;
(2)如PA=6,tan∠APB=
| 4 |
| 3 |
考点:切线的判定与性质
专题:
分析:(1)连接OA、OB,根据垂径定理得出AB⊥OP,推出AP=BP,∠APO=∠BPO,证△PAO≌△PBO,推出∠PBO=∠PAO=90°,根据切线的判定推出即可;
(2)延长AO即可直线PB于M,交⊙O于N,在Rt△MAP中,PA=6,tan∠APB=
=
,求出AM,由勾股定理求出PM=10,求出BM=4,设⊙O的半径为R,在Rt△OBM中,由勾股定理得出(8-R)2=R2+42,求出即可.
(2)延长AO即可直线PB于M,交⊙O于N,在Rt△MAP中,PA=6,tan∠APB=
| 4 |
| 3 |
| AM |
| AP |
解答: 解:(1)直线PB与⊙O的位置关系是相切,
解:(1)直线PB与⊙O的位置关系是相切,
理由是:连接OA、OB,
∵OP平分AB,OP过O,
∴AB⊥OP,
∴AP=BP,
∴∠APO=∠BPO,
∵PA切⊙O于A,
∴∠PAO=90°,
在△PAO和△PBO中
∴△PAO≌△PBO(SAS),
∴∠PBO=∠PAO=90°,
即OB⊥PB,
∴PB是⊙O的切线;
(2)
延长AO即可直线PB于M,交⊙O于N,
∵在Rt△MAP中,PA=6,tan∠APB=
=
,
∴AM=8,
由勾股定理得:PM=10,
∵PA=PB=6,
∴BM=10-6=4,
设⊙O的半径为R,
在Rt△OBM中,由勾股定理得:OM2=OB2+BM2,
则(8-R)2=R2+42,
解得:R=3,
即⊙O的半径长是3.
 解:(1)直线PB与⊙O的位置关系是相切,
解:(1)直线PB与⊙O的位置关系是相切,理由是:连接OA、OB,
∵OP平分AB,OP过O,
∴AB⊥OP,
∴AP=BP,
∴∠APO=∠BPO,
∵PA切⊙O于A,
∴∠PAO=90°,
在△PAO和△PBO中
|
∴△PAO≌△PBO(SAS),
∴∠PBO=∠PAO=90°,
即OB⊥PB,
∴PB是⊙O的切线;
(2)

延长AO即可直线PB于M,交⊙O于N,
∵在Rt△MAP中,PA=6,tan∠APB=
| 4 |
| 3 |
| AM |
| AP |
∴AM=8,
由勾股定理得:PM=10,
∵PA=PB=6,
∴BM=10-6=4,
设⊙O的半径为R,
在Rt△OBM中,由勾股定理得:OM2=OB2+BM2,
则(8-R)2=R2+42,
解得:R=3,
即⊙O的半径长是3.
点评:本题考查了垂径定理,切线的性质和判定,全等三角形的性质和判定,解直角三角形,勾股定理的应用,题目综合性比较强,有一定的难度.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
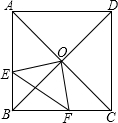 在正方形ABCD中,O是对角线的交点,过O作OE⊥OF,分别交AB、BC于E、F,若AE=4,CF=3,
在正方形ABCD中,O是对角线的交点,过O作OE⊥OF,分别交AB、BC于E、F,若AE=4,CF=3,