题目内容
一个不透明的口袋里装有分别标有汉字“先”、“驱”、“团”、“风”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,球上的汉字刚好是“团”的概率为多少?
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图的方法,求出甲取出的两个球上的汉字恰能组成“先驱”或“团风”的概率P1;
(3)乙从中任取一球,记下汉字后再放回袋中,然后再从中任取一球,记乙取出的两个球上的汉字恰能组成“先驱”或“团风”的概率为P2,指出P1,P2的大小关系(请直接写出结论,不必证明).
(1)若从中任取一个球,球上的汉字刚好是“团”的概率为多少?
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图的方法,求出甲取出的两个球上的汉字恰能组成“先驱”或“团风”的概率P1;
(3)乙从中任取一球,记下汉字后再放回袋中,然后再从中任取一球,记乙取出的两个球上的汉字恰能组成“先驱”或“团风”的概率为P2,指出P1,P2的大小关系(请直接写出结论,不必证明).
考点:列表法与树状图法
专题:
分析:(1)由一个不透明的口袋里装有分别标有汉字“先”、“驱”、“团”、“风”的四个小球,除汉字不同之外,球没有任何区别,直接利用概率公式求解即可求得答案;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与甲取出的两个球上的汉字恰能组成“先驱”或“团风”的情况,再利用概率公式即可求得答案;
(3)首先根据题意求得乙取出的两个球上的汉字恰能组成“先驱”或“团风”的概率P2的值,比较大小,即可求得答案.
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与甲取出的两个球上的汉字恰能组成“先驱”或“团风”的情况,再利用概率公式即可求得答案;
(3)首先根据题意求得乙取出的两个球上的汉字恰能组成“先驱”或“团风”的概率P2的值,比较大小,即可求得答案.
解答:解:(1)∵一个不透明的口袋里装有分别标有汉字“先”、“驱”、“团”、“风”的四个小球,除汉字不同之外,小球没有任何区别,
∴从中任取一个球,球上的汉字刚好是“团”的概率为:
;
(2)画树状图得:
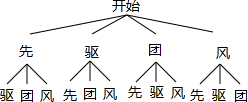
∵共有12种等可能的结果,甲取出的两个球上的汉字恰能组成“先驱”或“团风”的有4种情况,
∴甲取出的两个球上的汉字恰能组成“先驱”或“团风”的概率P1=
=
;
(3)∵乙从中任取一球,记下汉字后再放回袋中,然后再从中任取一球,
∴共有:4×4=16种等可能的结果,且乙取出的两个球上的汉字恰能组成“先驱”或“团风”的有4种情况,
∴乙取出的两个球上的汉字恰能组成“先驱”或“团风”的概率为P2=
=
.
∴P1>P2.
∴从中任取一个球,球上的汉字刚好是“团”的概率为:
| 1 |
| 4 |
(2)画树状图得:

∵共有12种等可能的结果,甲取出的两个球上的汉字恰能组成“先驱”或“团风”的有4种情况,
∴甲取出的两个球上的汉字恰能组成“先驱”或“团风”的概率P1=
| 4 |
| 12 |
| 1 |
| 3 |
(3)∵乙从中任取一球,记下汉字后再放回袋中,然后再从中任取一球,
∴共有:4×4=16种等可能的结果,且乙取出的两个球上的汉字恰能组成“先驱”或“团风”的有4种情况,
∴乙取出的两个球上的汉字恰能组成“先驱”或“团风”的概率为P2=
| 4 |
| 16 |
| 1 |
| 4 |
∴P1>P2.
点评:本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
下列运算正确的是( )
A、
| ||||||||||||
B、5+
| ||||||||||||
C、
| ||||||||||||
D、
|
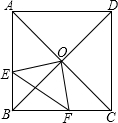 在正方形ABCD中,O是对角线的交点,过O作OE⊥OF,分别交AB、BC于E、F,若AE=4,CF=3,
在正方形ABCD中,O是对角线的交点,过O作OE⊥OF,分别交AB、BC于E、F,若AE=4,CF=3,
 如图,直线y=-
如图,直线y=-