题目内容
已知一元二次方程x2-(2a+1)+a2+a=0.
(1)求证:方程有两个不相等的实数根.
(2)若△ABC的两边AB、AC的长是原方程的两个实数根,第三边BC的长为5,当△ABC是等腰三角形时,求该三角形的周长.
(1)求证:方程有两个不相等的实数根.
(2)若△ABC的两边AB、AC的长是原方程的两个实数根,第三边BC的长为5,当△ABC是等腰三角形时,求该三角形的周长.
考点:根的判别式,根与系数的关系,三角形三边关系,等腰三角形的性质
专题:
分析:(1)证明判别式△>0,即可解决问题.
(2)首先求出方程的两个实数根,然后根据等腰三角形的定义,结合分类讨论的数学思想逐一解析,即可解决问题.
(2)首先求出方程的两个实数根,然后根据等腰三角形的定义,结合分类讨论的数学思想逐一解析,即可解决问题.
解答:解:(1)证明:∵△=[-(2a+1)]2-4(a2+a)
=4a2+4a+1-4a2-4a
=1>0,
∴方程有两个不相等的实数根.
(2)解方程x2-(2a+1)+a2+a=0,
得:两个根分别为a、a+1;
∵a≠a+1,
∴a与a+1只能是一个为腰,另一个为底;
若a为腰,则a+1为底,此时a=5,
∴该三角形的周长=16;
若a+1为腰,则a为底,此时a+1=5,a=4;
∴该三角形的周长=14.
=4a2+4a+1-4a2-4a
=1>0,
∴方程有两个不相等的实数根.
(2)解方程x2-(2a+1)+a2+a=0,
得:两个根分别为a、a+1;
∵a≠a+1,
∴a与a+1只能是一个为腰,另一个为底;
若a为腰,则a+1为底,此时a=5,
∴该三角形的周长=16;
若a+1为腰,则a为底,此时a+1=5,a=4;
∴该三角形的周长=14.
点评:该题主要考查了根的判别式、等腰三角形的定义及其应用问题;解题的关键是深入把握题意、大胆推理猜测、科学解答论证.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
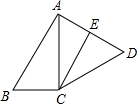 如图,四边形ABCD中,AC=CD,AB=2BC,∠BAC与∠B互余,CE∥BA,CE交AD于E,且CD2=CE2+DE2,求证:AD=
如图,四边形ABCD中,AC=CD,AB=2BC,∠BAC与∠B互余,CE∥BA,CE交AD于E,且CD2=CE2+DE2,求证:AD= 如图,已知∠BOC=2∠AOC,OD平分∠AOB,且∠COD=20°,求∠AOC的度数.
如图,已知∠BOC=2∠AOC,OD平分∠AOB,且∠COD=20°,求∠AOC的度数.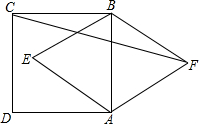 如图,正方形ABCD中,以AB为边分别在正方形内、外作等边△ABE,△ABF,则∠CFB=
如图,正方形ABCD中,以AB为边分别在正方形内、外作等边△ABE,△ABF,则∠CFB=