题目内容
5.已知关于x的一元二次方程ax2-(a+2)x+2=0.(1)不解方程,判别方程的根的情况;
(2)方程有两个不相等的正整数根时,求整数a的值.
分析 (1)由一元二次方程的定义可得出a≠0,再利用根的判别式△=b2-4ac,套入数据即可得出△=(a-2)2≥0,由此即可得出结论;
(2)结合(1)的结论可得出a≠2且a≠0,设方程的两个根分别为x1、x2,利用根与系数的关系可得出x1•x2=$\frac{2}{a}$,再根据x1、x2均为正整数,a为整数,即可得出结论.
解答 解:(1)∵方程ax2-(a+2)x+2=0是关于x的一元二次方程,
∴a≠0.
∵△=(a+2)2-4a×2=(a-2)2≥0,
∴当a=2时,方程有两个相等的实数根,当a≠2且a≠0时,方程有两个不相等的实数根.
(2)∵方程有两个不相等的正整数根,
∴a≠2且a≠0.
设方程的两个根分别为x1、x2,
∴x1•x2=$\frac{2}{a}$,
∵x1、x2均为正整数,
∴$\frac{2}{a}$为正整数,
∵a为整数,a≠2且a≠0,
∴a=1.
点评 本题考查了根的判别式以及根与系数的关系,解题的关键是:(1)找出△=(a-2)2≥0;(2)找出x1•x2=$\frac{2}{a}$为正整数.本题属于中档题,难度不大,解决该题型题目时,由方程的两根均为整数确定a的值是难点.

练习册系列答案
相关题目
20.2的倒数的相反数是( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | 2 | D. | -2 |
14.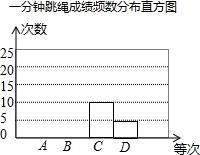 为备战体育中考,李明同学就自己平时1分钟跳绳的训练成绩,做了认真统计,并将训练成绩绘出了如下的频数分布表和频数分布直方图(不完整).(规定:1分钟跳绳120个以下成绩为D等;120-140个为C等;140-160个为B等;160个以上为A等)
为备战体育中考,李明同学就自己平时1分钟跳绳的训练成绩,做了认真统计,并将训练成绩绘出了如下的频数分布表和频数分布直方图(不完整).(规定:1分钟跳绳120个以下成绩为D等;120-140个为C等;140-160个为B等;160个以上为A等)
根据以上信息,解答下列问题:
(1)李明同学一共记录了50次平时测试的成绩;
(2)补全频数分布表和频数分布直方图;
(3)李明同学从篮球运球、足球运球、掷实心球、坐位体前屈、1分钟跳绳、立定跳远等六个项目中任选两项作为自己的考试项目,求恰好含有1分钟跳绳项目的概率.
一分钟跳绳成绩分布表
 为备战体育中考,李明同学就自己平时1分钟跳绳的训练成绩,做了认真统计,并将训练成绩绘出了如下的频数分布表和频数分布直方图(不完整).(规定:1分钟跳绳120个以下成绩为D等;120-140个为C等;140-160个为B等;160个以上为A等)
为备战体育中考,李明同学就自己平时1分钟跳绳的训练成绩,做了认真统计,并将训练成绩绘出了如下的频数分布表和频数分布直方图(不完整).(规定:1分钟跳绳120个以下成绩为D等;120-140个为C等;140-160个为B等;160个以上为A等)根据以上信息,解答下列问题:
(1)李明同学一共记录了50次平时测试的成绩;
(2)补全频数分布表和频数分布直方图;
(3)李明同学从篮球运球、足球运球、掷实心球、坐位体前屈、1分钟跳绳、立定跳远等六个项目中任选两项作为自己的考试项目,求恰好含有1分钟跳绳项目的概率.
一分钟跳绳成绩分布表
| 成绩等次 | 频数(人) | 频率 |
| D | 5 | 0.1 |
| C | 10 | 0.2 |
| B | 25 | 0.5 |
| A | 10 | 0.2 |
| 合计 | 50 | 1.00 |
 (1)计算:(2-π)0-$\sqrt{8}$×$\sqrt{2}$+($\frac{1}{3}$)-1
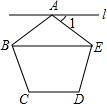
(1)计算:(2-π)0-$\sqrt{8}$×$\sqrt{2}$+($\frac{1}{3}$)-1 如图,直线l1∥l2,且被直线l3所截,若∠1=35°,∠P=90°,则∠2的度数为55°.
如图,直线l1∥l2,且被直线l3所截,若∠1=35°,∠P=90°,则∠2的度数为55°.