题目内容
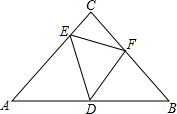 如图,已知Rt△ABC中,AC=BC,∠C=90°,D、E、F分别在AB、AC、BC边上,∠EDF=45°.
如图,已知Rt△ABC中,AC=BC,∠C=90°,D、E、F分别在AB、AC、BC边上,∠EDF=45°.(1)求证:△ADE∽△BFD;
(2)若D为AB中点,求证:∠AED=∠DEF.
考点:相似三角形的判定与性质
专题:证明题
分析:(1)由Rt△ABC中,AC=BC,∠C=90°,可得∠A=∠B=45°,又由∠EDF=45°,易证得∠AED=∠BDF,即可得△ADE∽△BFD;
(2)由△ADE∽△BFD,可得DE:DF=AE:BD,又由D为AB中点,易证得△DEF∽△AED,即可证得∠AED=∠DEF
(2)由△ADE∽△BFD,可得DE:DF=AE:BD,又由D为AB中点,易证得△DEF∽△AED,即可证得∠AED=∠DEF
解答:证明:(1)∵Rt△ABC中,AC=BC,∠C=90°,
∴∠A=∠B=45°,
∴∠AED+∠ADE=135°,
∵∠EDF=45°,
∴∠ADE+∠BDF=135°,
∴∠AED=∠BDF,
∴△ADE∽△BFD;
(2)∵△ADE∽△BFD,
∴DE:DF=AE:BD,
∵D为AB中点,
∴AD=BD,
∴DE:DF=AE:AD,
即DE:AE=DF:AD,
∵∠A=∠EDF=45°,
∴△DEF∽△AED,
∴∠AED=∠DEF.
∴∠A=∠B=45°,
∴∠AED+∠ADE=135°,
∵∠EDF=45°,
∴∠ADE+∠BDF=135°,
∴∠AED=∠BDF,
∴△ADE∽△BFD;
(2)∵△ADE∽△BFD,
∴DE:DF=AE:BD,
∵D为AB中点,
∴AD=BD,
∴DE:DF=AE:AD,
即DE:AE=DF:AD,
∵∠A=∠EDF=45°,
∴△DEF∽△AED,
∴∠AED=∠DEF.
点评:此题考查了相似三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知△ABC中,∠ACB=90°,CD⊥AB,∠A=30°,AB=40,求DB的长.
已知△ABC中,∠ACB=90°,CD⊥AB,∠A=30°,AB=40,求DB的长.
 如图是一块破碎的圆形木盖,试确定它的圆心.
如图是一块破碎的圆形木盖,试确定它的圆心. 如图,E,F在BC上,BE=CF,AB=CD,AB∥CD.求证:
如图,E,F在BC上,BE=CF,AB=CD,AB∥CD.求证:
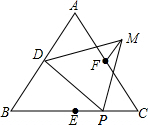 如图,D,E,F分别是正三角形ABC的边AB,BC,AC的中点,P为BC上任意一点,△DPM为正三角形.求证:PE=FM.
如图,D,E,F分别是正三角形ABC的边AB,BC,AC的中点,P为BC上任意一点,△DPM为正三角形.求证:PE=FM. 如图,PA=PB,PC是△PAB的中线,∠A=55°.求∠B的度数.
如图,PA=PB,PC是△PAB的中线,∠A=55°.求∠B的度数.
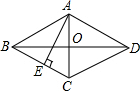 在菱形ABCD中,AE垂直平分BC,垂足为E,AB=4cm,求菱形的面积和对角线BD的长.
在菱形ABCD中,AE垂直平分BC,垂足为E,AB=4cm,求菱形的面积和对角线BD的长.