题目内容
如图①,已知点O是∠EPF的平分线上的一点,以点O为圆心的圆与角两边分别交于A,B和C,D四点.
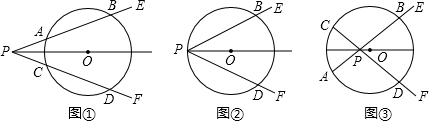
(1)求证:AB=CD;
(2)若角的顶点P在圆上,如图②,其他条件不变,结论成立吗?
(3)若角的顶点P在圆内,如图③,其他条件不变,结论成立吗?

(1)求证:AB=CD;
(2)若角的顶点P在圆上,如图②,其他条件不变,结论成立吗?
(3)若角的顶点P在圆内,如图③,其他条件不变,结论成立吗?
考点:垂径定理,角平分线的性质
专题:计算题
分析:(1)过O作OM⊥AB于M,ON⊥CD于N,连接OA、OC,根据角平分线性质得出ON=OM,根据勾股定理求出AM=CN,根据垂径定理得出AB=2AM,CD=2CN,即可得出答案;
(2)
(2)
解答: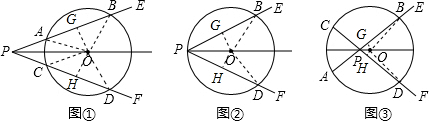 解:(1)相等.
解:(1)相等.
如图:
作OG⊥AB于G,OH⊥CD于H,连接OA,OC,OB,OD.
AG=BG,CH=DH,
∵∠EPO=∠FPO,
∴OG=OH.
在Rt△OBG和Rt△ODH中,
由HL定理得:△OBG≌△ODH,
∴GB=HD,
∴AB=CD;
(2)点P在圆上,结论成立:
顶点P在圆上,此时点P,A,C重合于点A,作OG⊥AB于G,OH⊥AD于H,
∴AG=GB,AH=HD,
∵∠EAO=∠DAO,
∴OG=OH.
在Rt△OAG和Rt△OAH中,由HL定理得:△OAG≌△OAH,
∴AG=AH,
∴AB=AD.
即点P在圆上,结论成立.
(3),顶点P在圆内,作OG⊥AB于G,OH⊥CD于H,则AG=GB,CH=HD,
∵∠EPO=∠FPO,
∴OG=OH,
∴GB=HD,
∴AB=CD.
即点P在圆内,结论成立.
 解:(1)相等.
解:(1)相等.如图:
作OG⊥AB于G,OH⊥CD于H,连接OA,OC,OB,OD.
AG=BG,CH=DH,
∵∠EPO=∠FPO,
∴OG=OH.
在Rt△OBG和Rt△ODH中,
由HL定理得:△OBG≌△ODH,
∴GB=HD,
∴AB=CD;
(2)点P在圆上,结论成立:
顶点P在圆上,此时点P,A,C重合于点A,作OG⊥AB于G,OH⊥AD于H,
∴AG=GB,AH=HD,
∵∠EAO=∠DAO,
∴OG=OH.
在Rt△OAG和Rt△OAH中,由HL定理得:△OAG≌△OAH,
∴AG=AH,
∴AB=AD.
即点P在圆上,结论成立.
(3),顶点P在圆内,作OG⊥AB于G,OH⊥CD于H,则AG=GB,CH=HD,
∵∠EPO=∠FPO,
∴OG=OH,
∴GB=HD,
∴AB=CD.
即点P在圆内,结论成立.
点评:本题考查的是垂径定理,先根据角平分线的性质定理,得到两条弦心距相等,然后再说明两条弦相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,小明上学的时间和行走的路程之间的函数关系.看图回答下列问题.
如图,小明上学的时间和行走的路程之间的函数关系.看图回答下列问题.
 如图,矩形ABCD的对角线AC,BD交于点O,EF⊥BD于点O,交AD于点E,交BC于点F,且EF=BF.
如图,矩形ABCD的对角线AC,BD交于点O,EF⊥BD于点O,交AD于点E,交BC于点F,且EF=BF. 如图,在△ABC中,∠1=∠B,AD=BD=6.
如图,在△ABC中,∠1=∠B,AD=BD=6.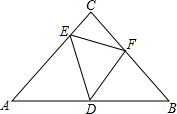 如图,已知Rt△ABC中,AC=BC,∠C=90°,D、E、F分别在AB、AC、BC边上,∠EDF=45°.
如图,已知Rt△ABC中,AC=BC,∠C=90°,D、E、F分别在AB、AC、BC边上,∠EDF=45°. 如图,用三个全等的等边三角形纸片,将它们拼成一个与等腰梯形全等的图案,可以怎样拼?在梯形中画出来.
如图,用三个全等的等边三角形纸片,将它们拼成一个与等腰梯形全等的图案,可以怎样拼?在梯形中画出来.