题目内容
如图，边长为a的三个正方形拼成一个矩形AEDF．
（1）△ABC与△DBA相似吗？
（2）∠1+∠2的度数是多少？
（1）△ABC与△DBA相似吗？
（2）∠1+∠2的度数是多少？
考点：相似三角形的判定与性质
专题：
分析：（1）根据勾股定理可求出AB的长，再根据相似三角形的判定方法即可证明△ABC与△DBA相似；
（2）由（1）可知△ABC与△DBA相似，所以∠2=∠BAC，根据三角形的外角和定理即可求出∠1+∠2的度数．
（2）由（1）可知△ABC与△DBA相似，所以∠2=∠BAC，根据三角形的外角和定理即可求出∠1+∠2的度数．
解答：（1）证明：∵边长为a的三个正方形拼成一个矩形AEDF，
∴AB=
=
a，
∵BC=a，BD=2a，
∴
=
，
∵∠ABC=∠DBA，
∴△ABC∽△DBA；
（2）解：∵△ABC∽△DBA，
∴∠2=∠BAC，
∵∠ABF=∠1+∠BAC=45°，
∴∠1+∠2=45°．
∴AB=
| AF2+BF2 |
| 2 |
∵BC=a，BD=2a，
∴
| AB |
| BD |
| BC |
| AB |
∵∠ABC=∠DBA，
∴△ABC∽△DBA；
（2）解：∵△ABC∽△DBA，
∴∠2=∠BAC，
∵∠ABF=∠1+∠BAC=45°，
∴∠1+∠2=45°．
点评：本题考查了矩形的性质、勾股定理的运用、相似三角形的判定和性质以及三角形外角和定理，题目的综合性较强，难度一般．
练习册系列答案
相关题目
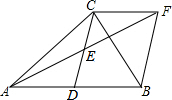如图，在△ABC中，D是AB的中点，E是CD的中点，延长AE到F点，使得E是AF的中点，连接BF，CF．求证：DC=BF．
如图，矩形ABCD的对角线AC，BD交于点O，EF⊥BD于点O，交AD于点E，交BC于点F，且EF=BF．
如图，在四边形ABCD中，∠A=∠C，∠ABC=∠ADC，求证：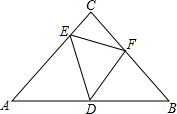
如图，已知Rt△ABC中，AC=BC，∠C=90°，D、E、F分别在AB、AC、BC边上，∠EDF=45°．
如图所示，有两个村庄A和B被一条河隔开，现要架一座桥（桥与河岸垂直），使A和B之间路程最短，请你设计一种方案．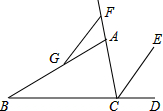
如图，CE平分∠ACD，F为CA延长线上一点，FG∥CE交AB于点G，∠ACD=100°，∠AGF=20°，求∠B的度数．