题目内容
13.若方程组中每个方程都是三元一次方程时,我们该如何确定先消哪个未知数?请以$\left\{\begin{array}{l}{2x+4y-3z=9}\\{3x-2y-4z=8}\\{5x-6y-5z=7}\end{array}\right.$为例进行探究.分析 ①+②×2得出8x-11z=25④,②×3-③得出4x-7z=17⑤,由④和⑤组成方程组,求出x、z的值,把x=-1,z=-3代入①求出y即可.
解答 解:先消去y,
$\left\{\begin{array}{l}{2x+4y-3z=9①}\\{3x-2y-4z=8②}\\{5x-6y-5z=7③}\end{array}\right.$
①+②×2得:8x-11z=25④,
②×3-③得:4x-7z=17⑤,
由④和⑤组成方程组:$\left\{\begin{array}{l}{8x-11z=25}\\{4x-7z=17}\end{array}\right.$,
解得:x=-1,z=-3,
把x=-1,z=-3代入①得:-2+4y+9=9,
解得:y=$\frac{1}{2}$,
所以原方程组的解为:$\left\{\begin{array}{l}{x=-1}\\{y=\frac{1}{2}}\\{z=-3}\end{array}\right.$.
点评 本题考查了三元一次方程组的应用,解此题的关键是能把三元一次方程组转化成二元一次方程组,此题是一道中档题目,难度适中.

练习册系列答案
相关题目
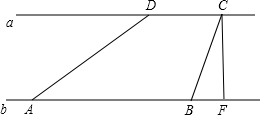 如图,河流两岸a、b平行,C、D是河岸a上间隔50米的两根电线杆,某人在河岸b上的A处测得∠DAE=30°,然后沿河岸走了100米到达B处,测得∠CBF=60°,则河流的宽度CF的值为43m(结果精确到个位,$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,河流两岸a、b平行,C、D是河岸a上间隔50米的两根电线杆,某人在河岸b上的A处测得∠DAE=30°,然后沿河岸走了100米到达B处,测得∠CBF=60°,则河流的宽度CF的值为43m(结果精确到个位,$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732) 如图,在平行四边形ABCD中,∠C=66°,点E为AD上一点,AB=BE,求∠EBC的度数.
如图,在平行四边形ABCD中,∠C=66°,点E为AD上一点,AB=BE,求∠EBC的度数.