题目内容
3.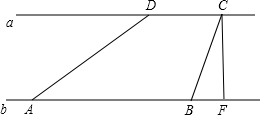 如图,河流两岸a、b平行,C、D是河岸a上间隔50米的两根电线杆,某人在河岸b上的A处测得∠DAE=30°,然后沿河岸走了100米到达B处,测得∠CBF=60°,则河流的宽度CF的值为43m(结果精确到个位,$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,河流两岸a、b平行,C、D是河岸a上间隔50米的两根电线杆,某人在河岸b上的A处测得∠DAE=30°,然后沿河岸走了100米到达B处,测得∠CBF=60°,则河流的宽度CF的值为43m(结果精确到个位,$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
分析 本题可将已知的条件构建到直角三角形中进行计算,过点C作CE∥AD,交AB于E,那么∠CEF=∠DAB=30°且AE=CD=50,根据观察发现,∠CBF=∠CEB+∠ECB=60°,而∠CEB=30°,那么∠ECB=∠CEB,那么CB=BE,直角三角形CBF中,有了CB的长,有锐角的度数,CF的值便可求出来.
解答  解:过点C作CE∥AD,交AB于E
解:过点C作CE∥AD,交AB于E
∵CD∥AE,CE∥AD
∴四边形AECD是平行四边形
∴AE=CD=50m,EB=AB-AE=50m,∠CEB=∠DAB=30°
又∠CBF=60°,故∠ECB=30°
∴CB=EB=50m
∴在Rt△CFB中,CF=CB•sin∠CBF=50•sin60°≈43m
答:河流的宽度CF的值为43m.
故答案为43m.
点评 本题考查了解直角三角形的应用,是将实际问题转化为直角三角形中的数学问题,可通过作辅助线构造直角三角形,再把条件和问题转化到这个直角三角形中,使问题解决.

练习册系列答案
相关题目
11.下列各式属于最简二次根式的是( )
| A. | $\sqrt{\frac{1}{3}}$ | B. | $\sqrt{12}$ | C. | $\sqrt{{x}^{2}+1}$ | D. | $\sqrt{4}$ |
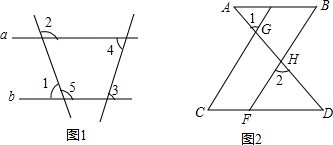 看图填空:
看图填空:
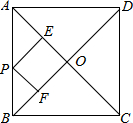 如图:正方形ABCD中,AC=10,P是AB上任意一点,PE⊥AC于E,PF⊥BD于F,则PE+PF=5.
如图:正方形ABCD中,AC=10,P是AB上任意一点,PE⊥AC于E,PF⊥BD于F,则PE+PF=5.