题目内容

8．二次函数的一般形式是y=ax2+bx+c（a≠0，a、b、c为常数），顶点坐标是（-$\frac{b}{2a}$，$\frac{4ac-{b}^{2}}{4a}$），对称轴是x=-$\frac{b}{2a}$．

分析 根据二次函数的形式与顶点解答．

解答 解：二次函数的一般形式是y=ax2+bx+c（a≠0，a、b、c为常数），
顶点坐标是（-$\frac{b}{2a}$，$\frac{4ac-{b}^{2}}{4a}$），对称轴是x=-$\frac{b}{2a}$．
故答案为：y=ax2+bx+c（a≠0，a、b、c为常数），（-$\frac{b}{2a}$，$\frac{4ac-{b}^{2}}{4a}$），x=-$\frac{b}{2a}$．

点评 本题考查了二次函数的解析式有三种形式：
（1）一般式：y=ax2+bx+c（a≠0，a、b、c为常数）；
（2）顶点式：y=a（x-h）2+k；
（3）交点式（与x轴）：y=a（x-x1）（x-x2）．

练习册系列答案
相关题目
18．（1）3（x-3）2=3-x   
（2）x2-2x=2x+1．
19．已知x=3是关于x的方程$\frac{4}{3}$x2-2a+1=0的一个根，则a的值是（　　）
A．5.5B．6C．6.5D．7
16．观察下列等式：$\frac{1}{{1}^{2}+2×1}$=$\frac{1}{2}$×（1-$\frac{1}{3}$），$\frac{1}{{2}^{2}+2×2}$=$\frac{1}{2}$×（$\frac{1}{2}$-$\frac{1}{4}$），$\frac{1}{{3}^{2}+2×3}$=$\frac{1}{2}$×（$\frac{1}{3}$-$\frac{1}{5}$），$\frac{1}{{4}^{2}+2×4}$=$\frac{1}{2}$×（$\frac{1}{4}$-$\frac{1}{6}$），…
根据你得出的规律写出第n个等式为$\frac{1}{{n}^{2}+2n}$=$\frac{1}{2}$×（$\frac{1}{n}$-$\frac{1}{n+2}$），并根据该规律计算：$\frac{1}{{1}^{2}+2×1}$+$\frac{1}{{2}^{2}+2×2}$+$\frac{1}{{3}^{2}+2×3}$+…+$\frac{1}{{8}^{2}+2×8}$=$\frac{29}{45}$．
3．（1）如图，将三角板放在正方形ABCD上，使三角板的直角顶点P在对角线AC上，一条直线边经过点B，另一条直角边交边DC于点E，求证：PB=PE．
（2）如图2，移动三角板，使三角板的直角顶点P在对角线AC上，一条直角边经过点B，另一条直角边交边DC的延长线于点E，PB=PE还成立吗？若成立，请证明，若不成立，请说明理由．
13．观察一列数：$\frac{1}{2}$，$-\frac{2}{5}$，$\frac{3}{10}$，$-\frac{4}{17}$，$\frac{5}{26}$，$-\frac{6}{37}$…根据规律，请你写出第8个数是-$\frac{8}{65}$．
20．四边形ABDC中，AB∥CD，∠BAC=90°，AB=AC，BE⊥AD交AC于E．

（1）求证：AE=CD；
（2）点G是AC上一点，若CG=AE，BE、FG的延长线交于点H，求证：EH=GH；
（3）点M在BC上，且BM=CF，MN∥AD，若AE=2，求BN的值．
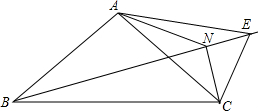17．如图，在△ABC中，AB=AC，∠ABC=α．过点B作一直线l，在l上取点E，使AE=AC，连接CE．∠CAE的平分线交BE于点N，连接NC．
（1）当α=45°时，AN、BN、CN之间的数量关系为$\sqrt{2}$AN=BN-CN
（2）当α=30°时．AN、BN、CN之间的数量关系为$\sqrt{3}$AN=BN-CN
（3）探究AN、BN、CN之间的数量关系为AN=$\frac{BN-CN}{cosα}$．（用含α的式子表示）．
18．已知m，n是方程x2-x-2016=0的两个实数根，则m2+n的值为于（　　）
A．1008B．2015C．2016D．2017

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网