题目内容
15.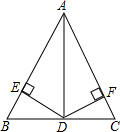 如图所示,已知在△ABC中,AD是∠BAC的平分线,BD=CD,DE⊥AB于E,DF⊥AC于F,求证:BE=FC.
如图所示,已知在△ABC中,AD是∠BAC的平分线,BD=CD,DE⊥AB于E,DF⊥AC于F,求证:BE=FC.
分析 根据角平分线的性质可得到DE=DF,再根据BD=DC,利用HL来判定Rt△DBE≌Rt△DCF,由全等三角形的性质即可得到BE=CF.
解答 解:∵AD是∠BAC的平分线,DE,DF分别垂直于AB,BC,
∴DE=DF,
在Rt△DBE和Rt△DCF中,
$\left\{\begin{array}{l}{DE=DF}\\{BD=BC}\end{array}\right.$,
∴Rt△DBE≌Rt△DCF(HL),
∴BE=CF.
点评 本题考查了三角形全等的判定及性质,用到的知识点是角平分线的性质和全等三角形的判定与性质,得到DE=DF是解决本题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
6.如国所示,为几何体的平面展开图,则从左到右,其对应的几何体名称分别为( )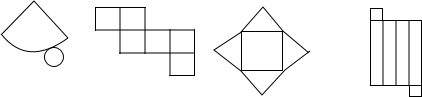

| A. | 圆锥,正方体,四棱锥,四梭柱 | B. | 圆柱,正方体,四棱锥,四梭柱 | ||
| C. | 圆锥,正方体,四棱柱,四梭锥 | D. | 圆柱,正方体,四棱柱,四梭锥 |
5.一次会议上,每两个参加会议的人都相互握一次手,有人统计一共握了36次手.设到会的人数为x人,则根据题意列方程为( )
| A. | x(x+1)=36 | B. | x(x-1)=36 | C. | 2x(x+1)=36 | D. | x(x-1)=36×2 |
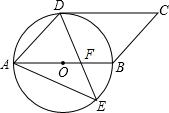 如图,四边形ABCD是平行四边形,以AB为直径的圆O经过点D,E是⊙O上一点,且∠AED=45°,DE交直径AB于点F.
如图,四边形ABCD是平行四边形,以AB为直径的圆O经过点D,E是⊙O上一点,且∠AED=45°,DE交直径AB于点F.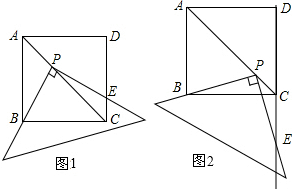
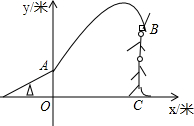 如图,杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线y=-$\frac{1}{3}$x2+2x+4的一部分.
如图,杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线y=-$\frac{1}{3}$x2+2x+4的一部分.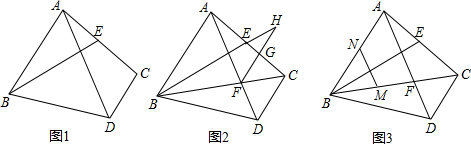
 A,B,C在一条直线上,△ABE与△BCD为等边三角形,AD与CE交于H,
A,B,C在一条直线上,△ABE与△BCD为等边三角形,AD与CE交于H,