题目内容
18.已知△ABC是边长为2的等边三角形,动点P在直线BC上运动(不与点B、C重合)(1)如图1,点P在线段BC上,作∠APQ=60°,PQ交AC于点Q,
①求证:△ABP∽△PCQ;
②若△APQ也与△PCQ相似,求此时AQ的长;
(2)如图2,点P在BC的延长线上,作∠APQ=60°,PQ的反向延长线相交于点D,是否存在点P,使△APD是等腰三角形?若存在,求出PC的长;若不存在,请说明理由.

分析 (1)①根据等腰直角三角形的性质得到∠B=∠C=60°,证明∠BAP=∠QPC,根据相似三角形的判定定理证明结论;②根据相似三角形的性质解答即可;
(2)根据等腰三角形的性质和相似三角形的判定定理证明△CAP∽△PAD,根据相似三角形的性质计算即可.
解答 解:(1)①∵∠BAC=90°,AB=AC=2,
∴∠B=∠C=60°,
∵∠BAP+∠APB=120°,
∠APB+∠QPC=120°,
∴∠BAP=∠QPC,
∴△ABP∽△PCQ;
②∵△APQ也与△PCQ相似,∠APQ=∠C=60°,
∴当∠CPQ=∠PAC时,∠AQP=∠PQC=90°,
∴∠PAQ=30°,
∴AP⊥BC,
∴AP=$\sqrt{3}$,
∴AQ=$\frac{3}{2}$;
当∠CPQ=∠AQP时,
∵∠CPQ+∠PQC=120°,
而∠AQP+∠CQP=180°,
∴不合题意,
∴AQ=$\frac{3}{2}$;
(2)存在,
∵∠ACB=60°,
∴∠CAP+∠APC=60°,
∵∠APQ=60°,
∴∠CAP+∠D=60°,
∴∠APC=∠D,
∴△CAP∽△PAD,
∴$\frac{AC}{AP}$=$\frac{PC}{PD}$,又AP=PD,
∴PC=AC=2.
点评 本题考查的是相似三角形的判定和性质、三角形的判定和性质,掌握相关的性质定理、灵活运用分情况讨论思想是解题的关键.

练习册系列答案
相关题目
6.下列运算正确的是( )
| A. | x3÷x2=x | B. | x3•x2=x6 | C. | x3-x2=x | D. | x3+x2=x5 |
13. 如图是一个正方体展开图,把展开图折叠成正方体后,“美”字一面相对面上的字是( )
如图是一个正方体展开图,把展开图折叠成正方体后,“美”字一面相对面上的字是( )
 如图是一个正方体展开图,把展开图折叠成正方体后,“美”字一面相对面上的字是( )
如图是一个正方体展开图,把展开图折叠成正方体后,“美”字一面相对面上的字是( )| A. | 云 | B. | 龙 | C. | 湖 | D. | 丽 |
9.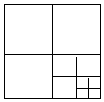 连结边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2017次操作后右下角的小正方形面积是( )
连结边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2017次操作后右下角的小正方形面积是( )
 连结边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2017次操作后右下角的小正方形面积是( )
连结边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2017次操作后右下角的小正方形面积是( )| A. | $\frac{1}{2017}$ | B. | ($\frac{1}{2}$)2017 | C. | ($\frac{1}{4}$)2017 | D. | 1-($\frac{1}{4}$)2017 |
10.已知|x|<a,x是整数,若满足条件的值有7个,则a的取值可能是( )
| A. | $\sqrt{8}$ | B. | π | C. | $\sqrt{17}$ | D. | 7 |
 在图中,A(1,3),B(-2,0)和C(2,-4)是一个直角三角形的顶点.
在图中,A(1,3),B(-2,0)和C(2,-4)是一个直角三角形的顶点.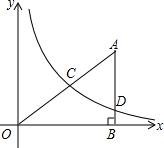 如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直于x轴,垂足为点B,反比例函数y=$\frac{k}{x}$(x>0)的图象经过AO上的点C,且$\frac{OC}{OA}=\frac{2}{3}$,与AB相交于点D,OB=6,AD=$\frac{5}{2}$,
如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直于x轴,垂足为点B,反比例函数y=$\frac{k}{x}$(x>0)的图象经过AO上的点C,且$\frac{OC}{OA}=\frac{2}{3}$,与AB相交于点D,OB=6,AD=$\frac{5}{2}$, 如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.则BC、EF的位置关系为平行.
如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.则BC、EF的位置关系为平行.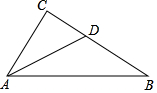 如图,Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D.若BC=16,CD=6,则AC=12.
如图,Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D.若BC=16,CD=6,则AC=12.