题目内容
9. 如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直于x轴,垂足为点B,反比例函数y=$\frac{k}{x}$(x>0)的图象经过AO上的点C,且$\frac{OC}{OA}=\frac{2}{3}$,与AB相交于点D,OB=6,AD=$\frac{5}{2}$,
如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直于x轴,垂足为点B,反比例函数y=$\frac{k}{x}$(x>0)的图象经过AO上的点C,且$\frac{OC}{OA}=\frac{2}{3}$,与AB相交于点D,OB=6,AD=$\frac{5}{2}$,(1)求点C的横坐标;
(2)求反比例函数y=$\frac{k}{x}$的解析式;
(3)求经过C、D两点的一次函数解析式.
分析 (1)如图,过点C作CE⊥x轴于点E,利用平行线截线段成比例求得点C的横坐标;
(2)设点D的坐标为(6,m)(m>0),则点A的坐标为(6,$\frac{5}{2}$+m),由点A的坐标表示出点C的坐标,根据C、D点在反比例函数图象上结合反比例函数图象上点的坐标特征即可得出关于k、m的二元一次方程,解方程即可得出结论;
(3)由m的值,可找出点C、D的坐标,设出过点C、D的一次函数的解析式为y=ax+b,由点C、D的坐标利用待定系数法即可得出结论
解答 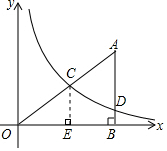 解:(1)如图,过点C作CE⊥x轴于点E,
解:(1)如图,过点C作CE⊥x轴于点E,
∵AB⊥x轴,
∴CE∥AB,
∴$\frac{OE}{OB}$=$\frac{OC}{OA}$.
又∵$\frac{OC}{OA}=\frac{2}{3}$,OB=6,
∴$\frac{OE}{6}$=$\frac{2}{3}$,则OE=4,
∴点C的横坐标是4;
(2)设点D的坐标为(6,m)(m>0),则点A的坐标为(6,$\frac{5}{2}$+m),
∵点C的坐标为(4,$\frac{5}{3}$+$\frac{2}{3}$m)
∵点C、点D均在反比例函数y=$\frac{k}{x}$(x>0)的函数图象上,
∴6m=4×($\frac{5}{3}$+$\frac{2}{3}$m),
解得:m=2.
故k=12
∴反比例函数的解析式为y=$\frac{12}{x}$.
(3)∵m=2,
∴点C的坐标为(4,3),点D的坐标为(6,2).
设经过点C、D的一次函数的解析式为y=ax+b,
则有$\left\{\begin{array}{l}{4a+b=3}\\{6a+b=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=5}\end{array}\right.$.
∴经过C、D两点的一次函数解析式为y=-$\frac{1}{2}$x+5.
点评 本题考查了反比例函数与一次函数的交点问题、反比例函数图象上点的坐标特征、解直角三角形以及待定系数法求函数解析式,解决该题型题目时,利用反比例函数图象上点的坐标特征找出方程组,通过解方程组得出点的坐标,再利用待定系数法求出函数解析式即可.

| A. | -4 | B. | 4 | C. | 8 | D. | 12 |
| A. | (-3a)2+4a2=a2 | B. | 3a2-(-2a)2=-a2 | C. | 3a•4a2=12a2 | D. | (3a2)2÷4a2=$\frac{3}{4}$a2 |
 如图,已知第一象限内的点A在反比例函数y=$\frac{2}{x}$的图象上,第二象限的点B在反比例函数y=$\frac{k}{x}$的图象上,且OA⊥OB,tanA=$\sqrt{2}$,则k的值为( )
如图,已知第一象限内的点A在反比例函数y=$\frac{2}{x}$的图象上,第二象限的点B在反比例函数y=$\frac{k}{x}$的图象上,且OA⊥OB,tanA=$\sqrt{2}$,则k的值为( )| A. | -3 | B. | -4 | C. | -6 | D. | -2$\sqrt{3}$ |
| A. | $\frac{3600}{x}$-$\frac{3600}{2x}$=10 | B. | $\frac{3600}{2x}$-$\frac{3600}{x}$=10 | C. | $\frac{3600}{x}$+$\frac{3600}{2x}$=10 | D. | 10(2x+x)=3600 |