题目内容
4.将全体正整数有规律地排成如图的“数阵”,观察处在“从左上角到右下角的对角线”上的数,依次是1,3,7,13,21,那么第n个数应是n2-n+1..| 1 | 2 | 9 | 10 | 25 | … |
| 4 | 3 | 8 | 11 | 24 | … |
| 5 | 6 | 7 | 12 | 23 | … |
| 16 | 15 | 14 | 13 | 22 | … |
| 17 | 18 | 19 | 20 | 21 | … |
| … | … | … | … | … | … |
分析 首先根据“数阵”图,设“从左上角到右下角的对角线”上的数,依次是a1,a2,a3,a4,a5,…,an,然后分别求出相邻两个数的差是多少,再把等式的左右两边分别相加,根据等差数列的求和公式,即可求出第n个数应是多少.
解答 解:设“从左上角到右下角的对角线”上的数,依次是a1,a2,a3,a4,a5,…,an,
则a1=1,
a2-a1=2,
a3-a2=4,
a4-a3=6,
…,
an-an-1=2(n-1),
把等式的左右两边分别相加,可得
an=1+2+4+6+…+2(n-1)
=1+2×(1+2+3+…+n-1)
=1+2×(1+n-1)×(n-1)÷2
=1+n(n-1)
=n2-n+1.
故答案为:n2-n+1.
点评 此题主要考查了探寻数字规律问题,注意观察总结规律,并能正确的应用规律,解答此题的关键是判断出:“从左上角到右下角的对角线”上的数中,相邻两个数的差分别是2、4、6、8、….

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
17.与-$\frac{1}{2}$乘积为1的数是( )
| A. | $\frac{1}{2}$ | B. | -2 | C. | 2 | D. | -$\frac{1}{2}$ |
9.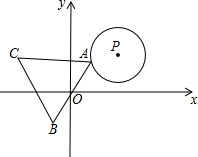 如图,⊙P在第一象限,半径为3.动点A沿着⊙P运动一周,在点A运动的同时,作点A关于原点O的对称点B,再以AB为边作等边三角形△ABC,点C在第二象限,点C随点A运动所形成的图形的面积为( )
如图,⊙P在第一象限,半径为3.动点A沿着⊙P运动一周,在点A运动的同时,作点A关于原点O的对称点B,再以AB为边作等边三角形△ABC,点C在第二象限,点C随点A运动所形成的图形的面积为( )
 如图,⊙P在第一象限,半径为3.动点A沿着⊙P运动一周,在点A运动的同时,作点A关于原点O的对称点B,再以AB为边作等边三角形△ABC,点C在第二象限,点C随点A运动所形成的图形的面积为( )
如图,⊙P在第一象限,半径为3.动点A沿着⊙P运动一周,在点A运动的同时,作点A关于原点O的对称点B,再以AB为边作等边三角形△ABC,点C在第二象限,点C随点A运动所形成的图形的面积为( )| A. | $\frac{{43\sqrt{3}}}{6}$ | B. | 27π | C. | $3\sqrt{3}π$ | D. | $\frac{{3\sqrt{3}}}{7}$π |
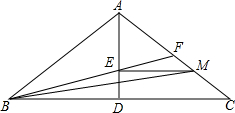 如图,在等腰三角形ABC中,AD⊥BC于点D,AD=3,DC=4,点M在线段AC上运动,ME⊥AD于点E,连结BE并延长交AC于点F,连结BM.设$\frac{CM}{AC}$=m(0<m<1),△BEM的面积为S.
如图,在等腰三角形ABC中,AD⊥BC于点D,AD=3,DC=4,点M在线段AC上运动,ME⊥AD于点E,连结BE并延长交AC于点F,连结BM.设$\frac{CM}{AC}$=m(0<m<1),△BEM的面积为S. 如图,直线a∥b,点B在直线b上,∠1=38°,∠ABC=90°,则∠2=52°.
如图,直线a∥b,点B在直线b上,∠1=38°,∠ABC=90°,则∠2=52°.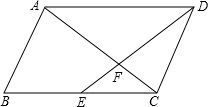 点E是平行四边形ABCD边BC的中点,平行四边形ABCD的面积是m,则四边形ABEF的面积是$\frac{5}{12}$m.
点E是平行四边形ABCD边BC的中点,平行四边形ABCD的面积是m,则四边形ABEF的面积是$\frac{5}{12}$m. 如图,小花同学设计了一个圆直径的测量器,标有刻度的尺子在O点钉在一起,并使它们保持垂直,在测直径时,把O点靠在圆周上,交圆E、F两点,读得刻度OE=8cm,OF=6cm,则圆的直径为10cm.
如图,小花同学设计了一个圆直径的测量器,标有刻度的尺子在O点钉在一起,并使它们保持垂直,在测直径时,把O点靠在圆周上,交圆E、F两点,读得刻度OE=8cm,OF=6cm,则圆的直径为10cm.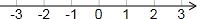 解不等式组$\left\{\begin{array}{l}x-1<2\\ 2x+9>3.\end{array}\right.$请结合题意填空,完成本小题的解答.
解不等式组$\left\{\begin{array}{l}x-1<2\\ 2x+9>3.\end{array}\right.$请结合题意填空,完成本小题的解答.