题目内容
13.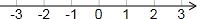 解不等式组$\left\{\begin{array}{l}x-1<2\\ 2x+9>3.\end{array}\right.$请结合题意填空,完成本小题的解答.
解不等式组$\left\{\begin{array}{l}x-1<2\\ 2x+9>3.\end{array}\right.$请结合题意填空,完成本小题的解答.(Ⅰ)解不等式①,得x<3;
(Ⅱ)解不等式②,得x>-3;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
(Ⅳ)原不等式组的解集为-3<x<3.
分析 根据不等式的性质求出每个不等式的解集,再在数轴上表示不等式的解集,最后求出不等式组的解集即可.
解答 解:$\left\{\begin{array}{l}{x-1<2①}\\{2x+9>3②}\end{array}\right.$
(I)解不等式①得:x<3,
(II)解不等式②得:x>-3,
(III)把不等式①和②的解集在数轴上表示出来: ;
;
(IV)原不等式组的解集为-3<x<3,
故答案为:x<3,x>-3,-3<x<3.
点评 本题考查了解一元一次不等式,解一元一次不等式组,在数轴上表示不等式的解集的应用,解此题的关键是能根据不等式的解集找出不等式组的解集,难度适中.

练习册系列答案
相关题目
4.将全体正整数有规律地排成如图的“数阵”,观察处在“从左上角到右下角的对角线”上的数,依次是1,3,7,13,21,那么第n个数应是n2-n+1..
| 1 | 2 | 9 | 10 | 25 | … |
| 4 | 3 | 8 | 11 | 24 | … |
| 5 | 6 | 7 | 12 | 23 | … |
| 16 | 15 | 14 | 13 | 22 | … |
| 17 | 18 | 19 | 20 | 21 | … |
| … | … | … | … | … | … |
5. 已知实数a,b在数轴上的位置如图,则下列等式成立的是( )
已知实数a,b在数轴上的位置如图,则下列等式成立的是( )
 已知实数a,b在数轴上的位置如图,则下列等式成立的是( )
已知实数a,b在数轴上的位置如图,则下列等式成立的是( )| A. | b-a>0 | B. | a+b>0 | C. | a-1>0 | D. | 1-b>0 |
8.计算(-6)÷(-1)的结果等于( )
| A. | 6 | B. | -6 | C. | $\frac{1}{6}$ | D. | -7 |
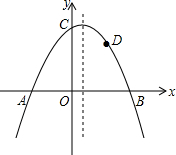 如图,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.
如图,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.
 如图所示,要使a∥b,需要添加一个条件,这个条件可以是∠1=∠3(答案不唯一).
如图所示,要使a∥b,需要添加一个条件,这个条件可以是∠1=∠3(答案不唯一).