题目内容
16.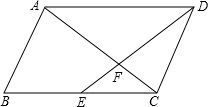 点E是平行四边形ABCD边BC的中点,平行四边形ABCD的面积是m,则四边形ABEF的面积是$\frac{5}{12}$m.
点E是平行四边形ABCD边BC的中点,平行四边形ABCD的面积是m,则四边形ABEF的面积是$\frac{5}{12}$m.
分析 设出△EFC的面积为a,根据△AFD∽△CFE和AD=2EC,求出△AFD的面积,根据DF=2FE,求出△DFC的面积,计算得到a=$\frac{1}{12}$m,得到答案.
解答 解:设△EFC的面积为a,
∵E是BC的中点,
∴BC=2EC,则AD=2EC,
∵AD∥BC,
∴△AFD∽△CFE,
∴△AFD的面积为4a,
∵DF=2FE,
∴△DFC的面积为2a,
∴△ADC的面积为6a,
则四边形ABEF的面积为5a,
又∵平行四边形ABCD的面积是m,即12a=m,a=$\frac{1}{12}$m,
∴四边形ABEF的面积$\frac{5}{12}$m.
故答案为:$\frac{5}{12}$m.
点评 本题考查的是面积的计算,掌握相似三角形的面积比等于相似比的平方是解题的关键,解答时,注意等高的两个三角形的面积比等于底的比.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
7.将正奇数按下表排成5列:
第一列第二列第三列第四列第五列
第一行 1 3 5 7
第二行 15 13 11 9
第三行 17 19 21 23
第四行 31 29 27 25
…
根据上面规律,2007应在( )
第一列第二列第三列第四列第五列
第一行 1 3 5 7
第二行 15 13 11 9
第三行 17 19 21 23
第四行 31 29 27 25
…
根据上面规律,2007应在( )
| A. | 125行,3列 | B. | 125行,2列 | C. | 251行,2列 | D. | 251行,5列 |
4.将全体正整数有规律地排成如图的“数阵”,观察处在“从左上角到右下角的对角线”上的数,依次是1,3,7,13,21,那么第n个数应是n2-n+1..
| 1 | 2 | 9 | 10 | 25 | … |
| 4 | 3 | 8 | 11 | 24 | … |
| 5 | 6 | 7 | 12 | 23 | … |
| 16 | 15 | 14 | 13 | 22 | … |
| 17 | 18 | 19 | 20 | 21 | … |
| … | … | … | … | … | … |
1.下列计算正确的是( )
| A. | a3+a2=a5 | B. | a0=1 | C. | (a2)3=a6 | D. | (-3)-2=-$\frac{1}{9}$ |
5. 已知实数a,b在数轴上的位置如图,则下列等式成立的是( )
已知实数a,b在数轴上的位置如图,则下列等式成立的是( )
 已知实数a,b在数轴上的位置如图,则下列等式成立的是( )
已知实数a,b在数轴上的位置如图,则下列等式成立的是( )| A. | b-a>0 | B. | a+b>0 | C. | a-1>0 | D. | 1-b>0 |
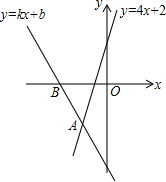 如图,经过点B(-2,0)的直线y=kx+b与直线y=4x+2相交于点A(-1,-2),则不等式kx+b<4x+2<0 的解集为-1<x<-$\frac{1}{2}$.
如图,经过点B(-2,0)的直线y=kx+b与直线y=4x+2相交于点A(-1,-2),则不等式kx+b<4x+2<0 的解集为-1<x<-$\frac{1}{2}$.