题目内容
9.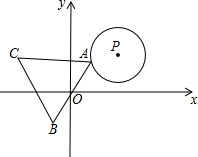 如图,⊙P在第一象限,半径为3.动点A沿着⊙P运动一周,在点A运动的同时,作点A关于原点O的对称点B,再以AB为边作等边三角形△ABC,点C在第二象限,点C随点A运动所形成的图形的面积为( )
如图,⊙P在第一象限,半径为3.动点A沿着⊙P运动一周,在点A运动的同时,作点A关于原点O的对称点B,再以AB为边作等边三角形△ABC,点C在第二象限,点C随点A运动所形成的图形的面积为( )| A. | $\frac{{43\sqrt{3}}}{6}$ | B. | 27π | C. | $3\sqrt{3}π$ | D. | $\frac{{3\sqrt{3}}}{7}$π |
分析 如图所示,点C随A运动所形成的图形为圆,根据等边三角形的性质求出CC′的长,即为圆的直径,求出圆的面积即可.
解答 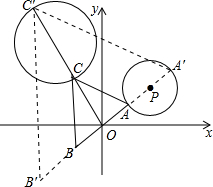 解:如图所示,点C随A运动所形成的图形为圆,可得OC=$\sqrt{3}$OA,OC′=$\sqrt{3}$OA′,
解:如图所示,点C随A运动所形成的图形为圆,可得OC=$\sqrt{3}$OA,OC′=$\sqrt{3}$OA′,
∴CC′=OC′-OC=$\sqrt{3}$(OA′-OA)=$\sqrt{3}$AA′=6$\sqrt{3}$,
∴点C随点A运动所形成的圆的面积为π×(3$\sqrt{3}$)2=27π,
故选B.
点评 此题考查了轨迹,以及等边三角形的性质,根据题意得出点C随A运动所形成的图形为圆是解本题的关键.

练习册系列答案
相关题目
4.将全体正整数有规律地排成如图的“数阵”,观察处在“从左上角到右下角的对角线”上的数,依次是1,3,7,13,21,那么第n个数应是n2-n+1..
| 1 | 2 | 9 | 10 | 25 | … |
| 4 | 3 | 8 | 11 | 24 | … |
| 5 | 6 | 7 | 12 | 23 | … |
| 16 | 15 | 14 | 13 | 22 | … |
| 17 | 18 | 19 | 20 | 21 | … |
| … | … | … | … | … | … |
1.下列计算正确的是( )
| A. | a3+a2=a5 | B. | a0=1 | C. | (a2)3=a6 | D. | (-3)-2=-$\frac{1}{9}$ |
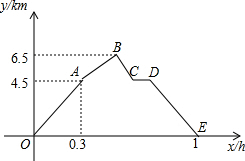 从甲地到乙地,先是一段平路,然后是一段上坡路,小明骑车从甲地出发,到达乙地后立即原路返回甲地,途中休息了一段时间,假设小明骑车在平路、上坡、下坡时分别保持匀速前进.已知小明骑车上坡的速度比在平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km.设小明出发x h后,到达离甲地y km的地方,图中的折线OABCDE表示y与x之间的函数关系.如果小明两次经过途中某一地点的时间间隔为0.12h,那么该地点离甲地5.7km.
从甲地到乙地,先是一段平路,然后是一段上坡路,小明骑车从甲地出发,到达乙地后立即原路返回甲地,途中休息了一段时间,假设小明骑车在平路、上坡、下坡时分别保持匀速前进.已知小明骑车上坡的速度比在平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km.设小明出发x h后,到达离甲地y km的地方,图中的折线OABCDE表示y与x之间的函数关系.如果小明两次经过途中某一地点的时间间隔为0.12h,那么该地点离甲地5.7km.