题目内容
6.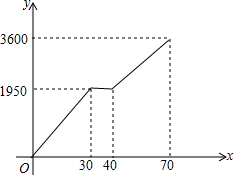 小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后40分钟后才乘上缆车,缆车的平均速度为180米/分.设小亮出发x分后行走的路程为y米.图中的折线表示小亮在整个行走过程中y随x的变化关系.
小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后40分钟后才乘上缆车,缆车的平均速度为180米/分.设小亮出发x分后行走的路程为y米.图中的折线表示小亮在整个行走过程中y随x的变化关系.(1)小亮行走的总路程是3600米,他途中休息了10分.
(2)分别求出小亮在休息前和休息后所走的路程段上的步行速度.
(3)当小颖到达缆车终点时,小亮离缆车终点的路程是多少?
分析 根据图象获取信息:
(1)小亮到达山顶用时70分钟,中途休息了10分钟,行程为3600米;
(2)休息前30分钟行走1950米,休息后10分钟行走(3600-1950)米.
(3)求小颖到达缆车终点的时间,计算小亮行走路程,求离缆车终点的路程.
解答 解:(1)根据图象知:小亮行走的总路程是3600米,他途中休息了10分钟.
故答案为 3600,10;
(2)小亮休息前的速度为:$\frac{1950}{30}=65$(米/分),
小亮休息后的速度为:$\frac{3600-1950}{70-40}=55$(米/分);
(3)小颖所用时间:$\frac{3600}{\frac{2}{180}}=10$(分),
小亮比小颖迟到70-40-10=20(分),
∴小颖到达终点时,小亮离缆车终点的路程为:20×55=1100(米).
点评 此题考查一次函数及其图象的应用,从图象中获取相关信息是关键.此题第3问难度较大.

练习册系列答案
相关题目
 如图,已知EF过?ABCD的顶点C,分别交AB、AD的延长线于E、F,且DF=3cm,DA=6cm,BE=4cm,求DC的长.
如图,已知EF过?ABCD的顶点C,分别交AB、AD的延长线于E、F,且DF=3cm,DA=6cm,BE=4cm,求DC的长.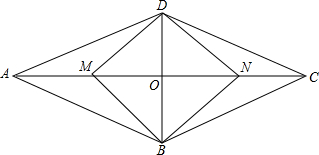 如图,菱形ABCD与矩形BMDN有公共对角线BD,M,N在AC上,且AC=4,BD=2,则AD:DM=$\sqrt{5}$:$\sqrt{2}$.
如图,菱形ABCD与矩形BMDN有公共对角线BD,M,N在AC上,且AC=4,BD=2,则AD:DM=$\sqrt{5}$:$\sqrt{2}$.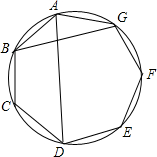 已知边长为1的正七边形ABCDEFG中,对角线AD,BG的长分别为a,b(a≠b),求证:(a+b)2(a-b)=ab2.
已知边长为1的正七边形ABCDEFG中,对角线AD,BG的长分别为a,b(a≠b),求证:(a+b)2(a-b)=ab2. 正方形ABCD边长为4,P(不与D重合)为DC边上一动点,设DP=x,求△APD的面积y关于x的函数,并写出x的取值范围.
正方形ABCD边长为4,P(不与D重合)为DC边上一动点,设DP=x,求△APD的面积y关于x的函数,并写出x的取值范围.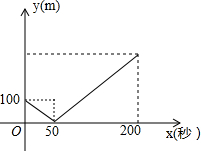 甲乙两人在一段长1200米的直线公路上进行跑步练习,起跑时乙在起点,甲在乙千米,若甲乙同时起跑至乙到达终点的过程中,甲乙之间的距离y(米)与时间t(秒)之间的函数关系如图所示,有下列说法:①甲的速度为4米/秒;②50秒时乙追上甲;③经过25秒时甲乙相距50米;④乙到达终点时甲距终点400米,其中正确的说法有( )
甲乙两人在一段长1200米的直线公路上进行跑步练习,起跑时乙在起点,甲在乙千米,若甲乙同时起跑至乙到达终点的过程中,甲乙之间的距离y(米)与时间t(秒)之间的函数关系如图所示,有下列说法:①甲的速度为4米/秒;②50秒时乙追上甲;③经过25秒时甲乙相距50米;④乙到达终点时甲距终点400米,其中正确的说法有( ) 如图,已知AD∥BC,∠DBC与∠C互余,BD平分∠ABC,∠A=112°,
如图,已知AD∥BC,∠DBC与∠C互余,BD平分∠ABC,∠A=112°,